Geometri fraktal dunia. Geometri fraktal adalah kode genetik alam semesta

Isi

Perkenalan

Konsep fraktal.................................................. ......................................................4

Sejarah munculnya fraktal…………………………………………………........6

Fraktal aljabar………………..…………………………….8

Kumpulan Maldebrod………………………………………...9
Julia mengatur…………………………………………………11
Kumpulan Newton (fraktal)…………………………………………………13
Fraktal (gelembung) Halley………………………………………..14

Penggunaan praktis fraktal……………………………...15

Kesimpulan……………………………………………………………………….19

Daftar referensi……………………………………………………………...…20

Perkenalan

Bahasa sains berubah dengan cepat di dunia modern. Sejarah perkembangan fisika sudah ada lebih dari satu abad. Selama ini, sejumlah besar fenomena alam yang beragam telah dipelajari, hukum dasar fisika telah ditemukan yang menjelaskan berbagai fakta eksperimental.

Kebanyakan sistem di alam menggabungkan dua sifat: pertama, mereka sangat besar, sering kali memiliki banyak segi, beragam dan kompleks, dan Kedua mereka terbentuk di bawah pengaruh sejumlah kecil hukum sederhana, dan berkembang lebih lanjut, dengan mematuhi hukum sederhana ini. Ini adalah yang paling banyak sistem yang berbeda, mulai dari kristal dan gugus sederhana (berbagai jenis gugus, seperti awan, sungai, gunung, benua, bintang), diakhiri dengan ekosistem dan objek biologis (dari daun pakis hingga otak manusia). Fraktal hanyalah objek seperti itu: di satu sisi, kompleks (mengandung banyak elemen tak terhingga), di sisi lain, dibangun menurut hukum yang sangat sederhana. Berkat sifat ini, fraktal memiliki banyak kesamaan dengan banyak objek alam. Tetapi fraktal lebih baik dibandingkan dengan objek alami karena fraktal mempunyai definisi matematis yang ketat dan dapat dideskripsikan dan dianalisis secara ketat. Oleh karena itu, teori fraktal memungkinkan untuk memprediksi laju pertumbuhan sistem perakaran tanaman, biaya tenaga kerja untuk mengeringkan rawa, ketergantungan massa jerami pada tinggi pucuk, dan masih banyak lagi. Ini adalah arah baru dalam matematika, yang telah merevolusi paradigma ilmiah, yang signifikansinya sebanding dengan teori relativitas dan mekanika kuantum. Objek geometri fraktal dengan caranya sendiri penampilan sangat berbeda dari bentuk geometris “biasa” yang biasa kita gunakan. Faktanya, ini merupakan terobosan dalam deskripsi matematis sistem yang sejak lama tidak dapat dijelaskan seperti itu.

Geometri fraktal bukanlah teori geometri “murni”. Ini lebih merupakan sebuah konsep, pandangan baru terhadap hal-hal yang diketahui, restrukturisasi persepsi yang memaksa peneliti untuk melihat dunia dengan cara yang baru.

Tujuan dari pekerjaan saya adalah untuk mengenal konsep "fraktal" dan variasinya "fraktal aljabar".

Konsep fraktal

Relatif baru-baru ini, dalam matematika, gambaran suatu benda muncul, lebih besar, namun mirip dengan garis. Beberapa ilmuwan merasa kesulitan untuk memahami konsep garis yang tidak memiliki lebar, sehingga mereka secara bertahap mulai mempelajarinya bentuk geometris dan struktur yang memiliki dimensi spasial pecahan. Kurva kontinu, yang semua turunannya, digantikan oleh kurva putus-putus atau sangat bergerigi. Contoh mencolok dari kurva tersebut adalah lintasan partikel Brown. Dari sinilah konsep fraktal muncul dalam sains.

Fraktal(Fraktus Latin - hancur, pecah, pecah) - bangun datar geometris kompleks yang memiliki sifat kesamaan diri, yaitu terdiri dari beberapa bagian, yang masing-masing mirip dengan keseluruhan gambar (Gbr. 1). Dalam pengertian yang lebih luas, fraktal dipahami sebagai kumpulan titik-titik dalam ruang Euclidean yang memiliki dimensi metrik pecahan (dalam pengertian Minkowski atau Hausdorff) atau dimensi metrik.

Beras. 1
Perlu dicatat bahwa kata "fraktal" bukanlah istilah matematika dan tidak memiliki definisi matematika ketat yang diterima secara umum. Ini dapat digunakan ketika gambar yang dimaksud memiliki salah satu properti berikut:

Ia memiliki struktur non-sepele di semua skala. Berbeda dengan bangun biasa (seperti lingkaran, elips, grafik fungsi lancar): Jika kita melihat pecahan kecil suatu bangun datar dengan skala yang sangat besar, maka akan terlihat seperti pecahan garis lurus. Untuk fraktal, peningkatan skala tidak berarti penyederhanaan struktur; pada semua skala kita akan melihat gambaran yang sama rumitnya.

Apakah mirip dengan diri sendiri atau kira-kira mirip dengan diri sendiri.

Ini memiliki dimensi metrik pecahan.

Banyak benda di alam yang mempunyai sifat fraktal, misalnya pantai, awan, tajuk pohon, sistem peredaran darah, dan sistem alveolar manusia atau hewan.
Fraktal, terutama di bidang pesawat, populer karena kombinasi keindahannya dengan kemudahan konstruksinya menggunakan komputer.

Sejarah fraktal

Studi tentang fraktal pada pergantian abad ke-19 dan ke-20 lebih bersifat episodik daripada sistematis, karena sebelumnya para ahli matematika terutama mempelajari objek-objek “baik” yang dapat dipelajari dengan menggunakan metode umum dan teori. Pada tahun 1872, ahli matematika Jerman Karl Weierstrass membuat contoh fungsi kontinu yang tidak dapat terdiferensiasi, yaitu tidak memiliki garis singgung pada titik mana pun. Namun konstruksinya sepenuhnya abstrak dan sulit dipahami. Oleh karena itu, pada tahun 1904, Helge von Koch dari Swedia menemukan kurva kontinu yang tidak memiliki garis singgung di mana pun, dan cukup mudah untuk digambar. Ternyata ia memiliki sifat fraktal. Salah satu varian dari kurva ini disebut “kepingan salju Koch”.
Ide kemiripan diri tokoh diambil oleh orang Prancis Paul Pierre Levy, mentor masa depan Benoit Mandelbrot. Pada tahun 1938, artikelnya “Kurva dan permukaan bidang dan spasial yang terdiri dari bagian-bagian yang serupa dengan keseluruhan” diterbitkan, yang menggambarkan fraktal lain - kurva Levy C. Semua fraktal yang tercantum di atas secara kondisional dapat diklasifikasikan sebagai satu kelas fraktal konstruktif (geometris).
Kelas lainnya adalah fraktal dinamis (aljabar), yang mencakup himpunan Mandelbrot. Penelitian pertama ke arah ini dimulai pada awal abad ke-20 dan dikaitkan dengan nama matematikawan Perancis Gaston Julia dan Pierre Fatou. Pada tahun 1918, karya Julia diterbitkan dengan iterasi kompleks fungsi rasional, yang menggambarkan himpunan Julia, seluruh keluarga fraktal yang berkerabat dekat dengan himpunan Mandelbrot. Karya ini dianugerahi penghargaan oleh Akademi Perancis, namun tidak memuat satu ilustrasi pun, sehingga tidak mungkin untuk mengapresiasi keindahan benda terbuka.

Ide pertama geometri fraktal muncul pada abad ke-19. Cantor, dengan menggunakan prosedur rekursif (berulang) sederhana, mengubah garis menjadi kumpulan titik-titik yang tidak terhubung (yang disebut Cantor Dust). Dia akan mengambil garis dan menghapus sepertiga bagian tengah dan kemudian mengulangi hal yang sama dengan bagian yang tersisa. (Gbr. 2)

Beras. 2

Peano menggambar garis khusus. (Gbr. 3)

Beras. 3

Untuk menggambarnya, Peano menggunakan algoritma berikut.

Langkah pertama, ia mengambil sebuah garis lurus dan menggantinya dengan 9 ruas yang 3 kali lebih pendek dari panjang garis aslinya (bagian 1 dan 2 gambar). Kemudian dia melakukan hal yang sama pada setiap segmen garis yang dihasilkan. Dan seterusnya tanpa batas. Keunikan garis tersebut adalah memenuhi seluruh bidang. Terbukti bahwa untuk setiap titik pada bidang terdapat titik yang termasuk dalam garis Peano.

Kurva Peano dan debu Cantor melampaui objek geometris biasa. Mereka tidak mempunyai dimensi yang jelas. Debu Cantor sepertinya dibangun berdasarkan garis lurus satu dimensi, tetapi terdiri dari titik-titik (dimensi 0). Dan kurva Peano dibangun berdasarkan garis satu dimensi, dan hasilnya adalah sebuah bidang. Di banyak bidang ilmu pengetahuan lainnya, muncul masalah yang penyelesaiannya membawa hasil yang aneh seperti yang dijelaskan di atas (gerakan Brown, harga saham).

Hingga abad ke-20, data tentang benda-benda aneh tersebut terakumulasi, tanpa ada upaya untuk mensistematisasikannya. Sampai Benoit Mandelbrot, bapak geometri fraktal modern dan kata fraktal, mempelajarinya. Secara bertahap membandingkan fakta, ia sampai pada penemuan arah baru dalam matematika - geometri fraktal.

Untuk membayangkan fraktal dengan lebih jelas, mari kita perhatikan contoh yang diberikan dalam buku B. Mandelbrot “The Fractal Geometry of Nature”, yang telah menjadi buku klasik - “Berapa panjang pantai Inggris?” Jawaban atas pertanyaan ini tidak sesederhana kelihatannya. Itu semua tergantung pada panjang alat yang digunakan. Dengan mengukur pantai menggunakan penggaris kilometer, mereka memperoleh panjang tertentu. Namun, banyak teluk dan semenanjung kecil yang terlewatkan, yang ukurannya jauh lebih kecil dari penggaris yang diukur. Dengan memperkecil ukuran penggaris menjadi 1 meter, ternyata panjang pantai akan menjadi lebih panjang. Apabila mengukur panjang tepian menggunakan penggaris milimeter, dengan memperhitungkan bagian-bagian yang lebih besar dari satu milimeter, maka panjangnya akan semakin besar. Akibatnya, jawaban atas pertanyaan yang tampaknya sederhana ini dapat membingungkan siapa pun - panjang pantai Inggris tidak ada habisnya.

Fraktal aljabar

Fraktal aljabar mendapatkan namanya karena dibuat berdasarkan rumus aljabar. Ada beberapa metode untuk memperoleh fraktal aljabar. Salah satu caranya adalah dengan menghitung fungsi berulang kali, dimanaz - bilangan kompleks, dan f adalah fungsi tertentu. Perhitungan fungsi ini berlanjut hingga kondisi tertentu terpenuhi. Dan jika kondisi ini terpenuhi, sebuah titik akan ditampilkan di layar. Dalam hal ini, nilai fungsi untuk titik berbeda pada bidang kompleks dapat memiliki perilaku berbeda:

cenderung tak terhingga seiring berjalannya waktu;

cenderung 0;
mengambil beberapa nilai tetap dan tidak melampauinya;
perilakunya kacau, tanpa tren apa pun.

3.1 Himpunan Mandelbrot

Himpunan Mandelbrot (salah satu objek fraktal paling terkenal) pertama kali dibuat (secara visual menggunakan komputer) oleh Benoit Mandelbrot pada musim semi tahun 1980 di pusat penelitian IBM. Thomas J.Watson. Dan meskipun penelitian terhadap objek-objek tersebut dimulai pada abad terakhir, penemuan himpunan ini dan peningkatan perangkat keras grafis komputerlah yang sangat mempengaruhi perkembangan geometri fraktal dan teori chaos. Jadi, apa himpunan Mandelbrot itu?

Pertimbangkan fungsi variabel kompleks. Ayo taruhdan pertimbangkan urutannya, di mana untuk apa saja. Barisan seperti itu dapat dibatasi (yaitu dapat terdapat r sedemikian sehingga untuk sembarang) atau “lari hingga tak terhingga” (yaitu untuk r > 0 apa pun yang ada). Himpunan Mandelbrot dapat didefinisikan sebagai himpunan bilangan kompleks c yang barisan tertentunya dibatasi. Sayangnya, tidak ada ekspresi analitik yang diketahui yang memungkinkan c tertentu menentukan apakah c tersebut termasuk dalam himpunan Mandelbrot atau tidak. Oleh karena itu, untuk membangun suatu himpunan, digunakan eksperimen komputer: mereka melihat himpunan titik-titik pada bidang kompleks dengan langkah tertentu, dan untuk setiap titik mereka melaksanakannya. sejumlah tertentu iterasi (temukan sejumlah anggota urutan) dan perhatikan “perilakunya”. (Gbr. 4).

Himpunan Mandelbrot terbukti terletak pada lingkaran dengan jari-jari r=2 dengan pusat di titik asal. Jadi, jika pada suatu langkah modulus suku berikutnya dari barisan tersebut melebihi 2, kita dapat segera menyimpulkan bahwa titik yang bersesuaian dengan c, yang mendefinisikan barisan ini, tidak termasuk dalam himpunan Mandelbrot.

Dengan mengurangi langkah pemindaian bilangan kompleks dan meningkatkan jumlah iterasi, kita dapat memperoleh gambar sedetail yang kita suka, namun selalu hanya perkiraan gambar dari himpunan tersebut.

Mari kita punya N warna, diberi nomor untuk kepastian dari 0 hingga N-1. Kita asumsikan, sekali lagi untuk kepastian, bahwa warna hitam mempunyai angka 0. Jika untuk suatu c tertentu setelah iterasi N-1 titiknya tidak melampaui lingkaran berjari-jari 2, kita asumsikan bahwa c termasuk dalam himpunan Mandelbrot dan catlah ini poin c berwarna hitam. Sebaliknya, jika pada langkah tertentu k (k Є ) titik berikutnya berada di luar lingkaran berjari-jari 2 (yaitu pada langkah ke-k kita menyadari bahwa titik tersebut “melarikan diri”), catlah titik tersebut dengan warna k.

Gambar yang indah diperoleh dengan pemilihan palet dan lingkungan himpunan yang berhasil (yaitu, di luar himpunan kita akan mendapatkan “titik berwarna”) (Gbr. 5, 6).

Beras. 4

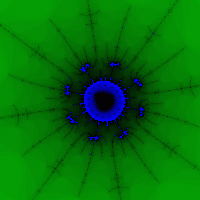
Beras. 5 Gambar. 6

3.2 Julia siap

Himpunan Julia, yang berkerabat dekat dengan himpunan Mandelbrot, dipelajari pada awal abad ke-20 oleh ahli matematika Gaston Julia dan Pierre Fatou (lihat). Pada tahun 1917-1919 mereka memperoleh hasil mendasar terkait iterasi fungsi variabel kompleks. Secara umum, fakta ini layak untuk didiskusikan secara terpisah dan merupakan contoh penelitian matematika yang mengesankan, beberapa dekade sebelumnya (para ilmuwan hanya dapat membayangkan secara kasar seperti apa objek yang mereka pelajari!), namun kami hanya akan menjelaskan metode untuk membangun Julia himpunan untuk fungsi variabel kompleks. Lebih tepatnya, kita akan membangun apa yang disebut. "mengisi set Julia".

Perhatikan sebuah persegi panjang (x 1 ;y 1 )-(X 2 ;y 2 ). Mari kita perbaiki konstanta c dan mulai melihat titik-titik persegi panjang yang dipilih dengan langkah tertentu. Untuk setiap titik, seperti dalam membangun himpunan Mandelbrot, kita akan melakukan serangkaian iterasi (semakin banyak jumlah iterasi, semakin akurat himpunan yang diperoleh). Jika setelah serangkaian iterasi titik tersebut tidak “melarikan diri” melewati batas lingkaran berjari-jari 2, kita akan mengecatnya dengan warna hitam, sebaliknya dengan warna dari palet. (Gbr. 7, 8, 9, 10).

Beras. 7

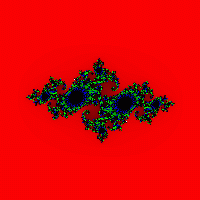
Gambar.8 Gambar. 9

Beras. 10

3.3 Kumpulan Newton (fraktal)

Jenis fraktal dinamis lainnya adalah fraktal Newton (disebut cekungan). (Gbr. 11). Rumus konstruksinya didasarkan pada metode penyelesaian persamaan nonlinier, yang ditemukan oleh ahli matematika hebat pada abad ke-17. Melamar rumus umum Metode Newton zn+1 = zn - f (zn)/f"(zn), n=0, 1, 2… untuk menyelesaikan persamaan f (x)=0 polinomial zk-a, kita memperoleh barisan titik-titik : zn+1 = (k-1)znk/kznk-1, n=0, 1, 2... Dengan memilih berbagai bilangan kompleks z0 sebagai perkiraan awal, kita akan memperoleh barisan-barisan yang konvergen ke akar-akar polinomial tersebut. mempunyai tepat k akar, maka seluruh bidang tersebut dibagi menjadi k bagian – daerah tarikan akar. Batas-batas bagian tersebut mempunyai struktur fraktal.

Beras. sebelas

3.4 Fraktal (gelembung) Halley

Fraktal seperti itu diperoleh jika, sebagai aturan untuk membangun fraktal dinamis, rumus Halley digunakan untuk menemukan nilai perkiraan akar suatu fungsi. (Gbr. 12).

Metode ini terdiri dari serangkaian iterasi:

Ide metode ini hampir sama dengan yang digunakan untuk menggambar fraktal dinamis: kita mengambil beberapa nilai awal (seperti biasa, di sini kita bicarakan nilai variabel dan fungsi) dan terapkan rumus tersebut berkali-kali, sehingga diperoleh barisan angka. Hampir selalu konvergen ke salah satu angka nol dari fungsi tersebut (yaitu, nilai variabel di mana fungsi tersebut bernilai 0). Metode Halley, meskipun rumusnya rumit, berhasil lebih efektif dibandingkan metode tersebut : Urutan konvergen ke fungsi nol lebih cepat.

Beras. 12

Penerapan praktis fraktal

Fraktal semakin banyak digunakan dalam sains. Alasan utama untuk ini adalah penjelasannya dunia nyata terkadang bahkan lebih baik daripada fisika atau matematika tradisional. Berikut beberapa contohnya.

Sistem komputer

Dari semua gambar yang dapat dibuat oleh komputer, hanya sedikit yang dapat menyaingi gambar fraktal dalam hal keindahan sesungguhnya.

Paling penggunaan yang berguna Fraktal dalam ilmu komputer adalah kompresi data fraktal. Jenis kompresi ini didasarkan pada kenyataan bahwa dunia nyata digambarkan dengan baik oleh geometri fraktal. Pada saat yang sama, gambar dikompresi jauh lebih baik dibandingkan dengan metode konvensional (seperti jpeg atau gif). Keuntungan lain dari kompresi fraktal adalah ketika gambar diperbesar, tidak ada efek pikselasi (memperbesar ukuran titik ke ukuran yang mendistorsi gambar). Dengan kompresi fraktal, setelah diperbesar, gambar sering kali terlihat lebih baik dari sebelumnya.

Mekanika fluida

Studi tentang turbulensi arus telah diadaptasi dengan sangat baik

fraktal. Aliran turbulen bersifat kacau sehingga sulit untuk dimodelkan secara akurat. Dan di sini transisi ke representasi fraktal membantu, yang sangat memudahkan pekerjaan para insinyur dan fisikawan, memungkinkan mereka untuk lebih memahami dinamika aliran kompleks.

Dengan menggunakan fraktal, Anda juga dapat menyimulasikan api.

Bahan berpori terwakili dengan baik dalam bentuk fraktal karena memiliki geometri yang sangat kompleks. Ini digunakan dalam ilmu perminyakan.

Telekomunikasi

Untuk mengirimkan data jarak jauh, antena dengan

bentuk fraktal, yang sangat mengurangi ukuran dan beratnya. Fraktal digunakan untuk menggambarkan kelengkungan permukaan. Permukaan yang tidak rata ditandai dengan kombinasi dua fraktal yang berbeda.
Obat

Interaksi biosensori. Denyut jantung.
Biologi

Pemodelan proses chaos, khususnya saat mendeskripsikan model populasi.
Nanoteknologi

Dalam kasus nanoteknologi, fraktal juga berperan peran penting, karena, karena pengorganisasian mandiri secara hierarkis, banyak sistem nano memiliki dimensi non-integer, yaitu fraktal dalam sifat geometris, fisikokimia, atau fungsionalnya. Misalnya, contoh mencolok dari sistem fraktal kimia adalah molekul "dendrimer » . (Gbr. 13)

Beras. 13

literatur

Di antara karya sastra temukan yang memiliki sifat fraktal tekstual, struktural, atau semantik. Dalam fraktal teks, unsur-unsur teks berpotensi diulang tanpa henti (“Pendeta mempunyai seekor anjing...”, “Perumpamaan filsuf yang bermimpi bahwa ia adalah seekor kupu-kupu yang bermimpi bahwa ia adalah seorang filsuf yang bermimpi...” dan teks dengan ekstensi (“Rumah yang dia bangun Jack”)

Dalam fraktal struktural, skema teks berpotensi fraktal: karangan bunga soneta (15 puisi), karangan bunga soneta (211 puisi), karangan bunga soneta (2455 puisi).

Kesimpulan

Fraktal adalah objek dengan kompleksitas tak terbatas, memungkinkan Anda melihat detailnya dari dekat maupun dari jauh. Bumi adalah contoh klasik objek fraktal. Dari luar angkasa terlihat seperti bola. Jika kita mendekatinya, kita akan menemukan lautan, benua, garis pantai, dan barisan pegunungan. Mari kita lihat pegunungan lebih dekat - detail yang lebih halus akan terlihat: sebidang tanah di permukaan gunung, dalam skalanya, sama rumit dan tidak ratanya dengan gunung itu sendiri. Dan pembesaran yang lebih besar lagi akan memperlihatkan partikel-partikel kecil tanah, yang masing-masing merupakan objek fraktal.

Sebagai kesimpulan, saya ingin mengatakan bahwa setelah fraktal ditemukan, menjadi jelas bagi banyak ilmuwan bahwa bentuk geometri Euclidean lama yang baik jauh lebih rendah daripada kebanyakan objek alam karena tidak adanya ketidakteraturan, ketidakteraturan, dan ketidakpastian di dalamnya. Ada kemungkinan bahwa ide-ide baru geometri fraktal akan membantu mempelajari banyak fenomena misterius alam sekitar. Saat ini, fraktal dengan cepat menyerang banyak bidang fisika, biologi, kedokteran, sosiologi, dan ekonomi. Metode pemrosesan gambar dan pengenalan pola yang menggunakan konsep-konsep baru memungkinkan peneliti menggunakan peralatan matematika ini untuk mendeskripsikan secara kuantitatif sejumlah besar objek dan struktur alam.

Bibliografi

1. Pengenalan fraktal,

2. Zhikov V.V. Di set Julia. // Ilmu pengetahuan alam modern: Ensiklopedia: Dalam 10 jilid T.1: Matematika. Mekanika. M., 2000.

3. Zhikov V.V.Fraktal. // Ilmu pengetahuan alam modern: Ensiklopedia: Dalam 10 jilid T.1: Matematika. Mekanika. M., 2000.

4. Mandelbrot B. Geometri alam fraktal. – M: Lembaga Penelitian Komputer, 2002.

5. Morozov A.D. Pengantar teori fraktal -Moscow-Izhevsk: Institute of Computer Research, 2002, 160pp.

6. Fraktal dinamis (aljabar) // Elemen.. URL:http:// elemen. ru/ poster/ fraktal/ dinamis

7. Fraktal dinamis (aljabar) // Elemen.. URL:http:// elementy.ru/posters/fractals/Mandelbrot#nop

8. Fraktal aljabar // Fraktal.. URL:http://rusproject.narod.ru/article/fractals.htm

Pada Bab 6 dan 7, kami memperkenalkan kurva Koch dan Peano dengan menggunakan geomorfologi untuk membantu kami, namun penerapan teori fraktal yang paling signifikan berada di bidang yang agak berbeda. Secara perlahan mendekati tren utama dalam sains, dalam bab ini (dan dua berikutnya) kita akan membahas dua pertanyaan tentang kekunoan, kepentingan, dan kompleksitas yang luar biasa.

Distribusi bintang, galaksi, gugus galaksi, dan hal-hal serupa telah lama memesona baik para amatir maupun spesialis, namun pengelompokan masih berada di luar lingkup astronomi, dan astrofisika secara umum. alasan utama adalah bahwa belum ada yang mampu menjelaskan mengapa distribusi materi mematuhi hukum hierarki yang tidak teratur – setidaknya dalam rentang skala tertentu. Dalam banyak karya yang membahas topik ini, kita dapat menemukan penyebutan fenomena pengelompokan, tetapi dalam studi teoretis yang serius, fenomena ini biasanya disembunyikan dengan tergesa-gesa, dengan alasan bahwa galaksi tersebar cukup merata - pada skala yang melebihi ambang batas yang besar namun tidak ditentukan. .

Melihat situasi ini dari sudut pandang yang kurang mendasar, kita dapat mengatakan bahwa keengganan untuk menangani hal-hal yang tidak beraturan berasal dari kurangnya alat untuk mendeskripsikannya secara matematis. Ahli statistik diharuskan memilih di antara dua asumsi, yang mana hanya satu yang dapat dianggap teruji secara menyeluruh (homogenitas asimtotik). Apakah mengherankan jika hasilnya, secara halus, tidak meyakinkan?

Namun, pertanyaan-pertanyaannya sedemikian rupa sehingga sulit untuk diabaikan. Saya pikir sangatlah penting - bersamaan dengan terus mencoba menjelaskan pengelompokan - untuk menemukan cara untuk mendeskripsikannya dan memodelkan realitas secara murni. sarana geometris. Dengan mendekati topik ini dari perspektif fraktal dalam beberapa bab esai ini, kami berharap dapat menunjukkan melalui model eksplisit bahwa bukti menunjukkan tingkat pengelompokan yang jauh melampaui batas yang ditetapkan oleh model yang ada.

Bab ini harus dianggap sebagai pengantar: di sini kita akan berkenalan dengan salah satu teori yang sangat berpengaruh tentang pembentukan bintang dan galaksi yang dikemukakan oleh Hoyle, dengan model formal dasar distribusinya, yang kita miliki kepada Fournier d'Albu (model ini juga dikenal sebagai model Charlier), dan, yang paling penting, kita akan memperoleh beberapa data empiris. Kami akan menunjukkan bahwa baik teori maupun data dapat diinterpretasikan dalam istilah konsep debu fraktal invarian skala. Saya bersikeras bahwa distribusi galaksi dan bintang mencakup zona kesamaan diri tertentu, yang di dalamnya dimensi fraktal memenuhi ketidaksetaraan. Selain itu, alasan teoritis mengapa seseorang dapat mengharapkan , dan, sebagai konsekuensinya, membahas mengapa nilai yang diamati adalah .

Pengumuman. Di Bab 22, kita akan menggunakan alat fraktal untuk meningkatkan pemahaman kita tentang makna prinsip kosmologis, mempertimbangkan bagaimana prinsip tersebut dapat dan harus dimodifikasi, dan mempelajari mengapa modifikasi tersebut memerlukan keacakan. Kami akan menunda pembahasan cluster dalam model yang ditingkatkan hingga Bab 22, 23, dan 32 hingga 35.

APAKAH MUNGKIN BERBICARA TENTANG GLOBALkepadatanURUSAN?

Mari kita mulai dengan melihat lebih dekat konsep kepadatan materi global. Seperti halnya garis pantai, segala sesuatu di sini, pada pandangan pertama, terlihat sangat sederhana, tetapi kenyataannya sangat cepat - dan sangat menarik - menjadi membingungkan. Untuk menentukan dan mengukur massa jenis, seseorang memulai dengan massa yang terkonsentrasi di dalam bola berjari-jari yang pusatnya bertepatan dengan pusat bumi. Ini memperkirakan perkiraan kepadatan, yang didefinisikan sebagai

Setelah ini, nilainya cenderung tak terhingga, dan kepadatan global didefinisikan sebagai batas konvergensi perkiraan kepadatan dalam kasus ini.

Namun, apakah kepadatan global harus menyatu hingga mencapai batas positif dan terbatas? Jika ya, maka kecepatan konvergensi seperti itu masih menyisakan banyak hal yang tidak diinginkan, dan itu tidak terlalu berarti. Selain itu, perkiraan kepadatan maksimum, jika dipertimbangkan dalam perspektif waktu, berperilaku agak aneh. Ketika kedalaman teleskopik alam semesta meningkat, perkiraan kepadatannya menurun secara sistematis. Menurut de Vaucouleurs, selalu terjadi penurunan. Indeks yang diamati kurang dari 3 - dalam perkiraan terbaik.

De Vaucouleurs mengajukan tesis bahwa perilaku perkiraan nilai kepadatan mencerminkan kenyataan, artinya . Rumus ini mengingatkan kita pada hasil klasik untuk bola berjari-jari yang tertanam dalam ruang dimensi Euclidean - volume bola tersebut. Pada Bab 6, kita menemukan rumus yang sama untuk kurva Koch, dengan satu-satunya perbedaan bahwa indikatornya bukanlah dimensi Euclidean, melainkan dimensi fraktal pecahan. Dan di Bab 8 kita mendapatkan rumus minuman Cantor pada sumbu waktu (di sini).

Semua preseden ini memaksa (dan terus-menerus) untuk berasumsi bahwa eksponen de Vaucouleurs tidak lebih dari sebuah dimensi fraktal.

APAKAH BINTANG DALAM RANGE INVARIAN SKALA?

Jelasnya, kisaran invariansi skala yang memenuhi ketidaksetaraan tidak boleh mencakup objek dengan batas yang jelas - seperti planet. Namun apakah bintang termasuk di dalamnya? Menurut data yang diperoleh Webbick dan disajikan di dalamnya, massa Bima Sakti di dalam bola radus dapat direpresentasikan dalam bentuk , yang nilainya diekstrapolasi dari galaksi. Namun, kami akan melanjutkan diskusi kami hanya dalam konteks galaksi.

APAKAH RANGE INVARIAN SKALA MEMILIKI THRESHOLD ATAS?

Pertanyaan tentang seberapa jauh rentang jangkauan tersebut menuju skala yang sangat besar sangatlah kontroversial, dan dalam Akhir-akhir ini dia menarik perhatian pada dirinya sendiri lagi. Banyak penulis yang secara eksplisit menyatakan atau menyiratkan bahwa rentang ini memungkinkan adanya batas terluar yang sesuai dengan ukuran gugus galaksi. Penulis lain menyatakan ketidaksetujuannya dengan pendapat ini. De Vaucouleurs berpendapat bahwa “pengelompokan galaksi, dan mungkin semua bentuk materi lainnya, merupakan ciri dominan struktur Alam Semesta pada semua skala yang dapat diamati, tanpa ada indikasi adanya perkiraan homogenitas; kepadatan rata-rata materi terus berkurang seiring dengan diperhitungkannya volume ruang yang lebih besar, dan kita tidak memiliki alasan yang terverifikasi secara eksperimental untuk percaya bahwa tren ini tidak meluas pada jarak yang lebih jauh dan kepadatan yang lebih rendah.”

Perdebatan antara kedua aliran ini tentunya sangat menarik dan penting – bagi kosmologi, namun tidak bagi esai kami. Sekalipun rentang di mana , memiliki batasan di kedua sisi, keberadaannya cukup signifikan untuk membenarkan studi yang paling cermat.

Bagaimanapun, Alam Semesta (seperti halnya bola benang yang kita bicarakan di Bab 6) tampaknya memiliki sejumlah dimensi efektif yang berbeda. Jika kita mulai dengan skala berdasarkan urutan jari-jari bumi, maka dimensi pertama yang kita temui adalah 3 (inilah dimensinya padatan dengan batas yang jelas). Selanjutnya, dimensinya turun menjadi 0 (karena materi dianggap sebagai sekelompok titik terisolasi). Berikutnya adalah bagian yang sangat menarik, ditandai dengan dimensi nontrivial tertentu yang memenuhi ketimpangan. Jika pengelompokan invarian skala berlanjut hingga tak terhingga, maka rangkaian dimensi efektif berakhir pada nilai terakhir ini. Jika ada ambang batas eksternal yang terbatas, maka interval dimensi keempat ditambahkan ke daftar, di mana titik-titik tersebut kehilangan individualitasnya, dan kita memiliki gas homogen di tangan kita, yaitu dimensi kembali ke 3 lagi.

Gagasan yang paling naif adalah bahwa galaksi-galaksi tersebar secara merata di alam semesta. Dalam hal ini, barisan dimensi D direduksi menjadi tiga nilai: 3, 0 dan lagi 3.

< Общая теория относительности утверждает, что при отсутствии материи локальная геометрия пространства стремится стать плоской и евклидовой, в то время как присутствие материи переводит ее в локально риманову. Здесь мы можем говорить о глобально плоской Вселенной, размерность которой равна 3 с локальными значениями . Такой тип возмущений описан в , довольно туманной работе, автор которой приводит (с. 312) пример построения кривой Коха (см. главу 6), не ссылаясь при этом на самого Коха.

ALAM SEMESTA FOURNIER

Yang harus kita lakukan adalah membuat fraktal yang memenuhi aturan dan melihat kesesuaiannya dengan pandangan umum tentang Alam Semesta. Model rinci pertama semacam ini diusulkan oleh E. E. Fournier d'Albom (lihat Bab 40).Meskipun buku Fournier sebagian besar merupakan fiksi yang disamarkan sebagai penelitian ilmiah, buku ini mengandung beberapa pertimbangan yang sangat menarik yang akan segera kita bahas.Pertama, tampaknya saya, kita harus menjelaskan struktur yang diusulkan oleh Fournier.

Kami memulai konstruksi dengan segi delapan biasa, yang proyeksinya ditunjukkan di tengah Gambar. 141. Proyeksi menunjukkan empat sudut sebuah persegi, yang diagonalnya adalah 12 "satuan", dan pusat dari persegi tersebut. Namun, segi delapan memiliki dua titik lagi di atas dan di bawah bidang kita pada garis tegak lurus yang ditarik melalui pusat persegi, pada jarak yang sama yaitu 6 “satuan” dari pusat tersebut.

Selanjutnya, setiap titik digantikan oleh bola berjari-jari 1, yang akan kita anggap sebagai “agregat bintang orde nol”. Bola terkecil yang berisi ketujuh bola asli akan disebut “agregat bintang orde pertama”. Agregat orde kedua diperoleh dengan menambah agregat orde pertama sebanyak satu faktor dan mengganti setiap bola baru berjari-jari 7 dengan salinan agregat orde pertama. Demikian pula, agregat orde ketiga diperoleh dengan menambah agregat orde kedua sebanyak satu faktor dan mengganti masing-masing bola dengan salinan agregat orde kedua. Dan seterusnya.

Singkatnya, ketika bertransisi antara tatanan agregasi yang berdekatan, jumlah titik dan jari-jari bola bertambah satu kali lipat. Akibatnya, untuk nilai apa pun yang merupakan jari-jari agregat apa pun, fungsi yang menentukan jumlah titik yang terdapat dalam bola berjari-jari berbentuk . Untuk fungsi perantara, fungsinya mengambil nilai lebih kecil (mencapai ), namun menurut kecenderungan umum, .

Dimungkinkan juga untuk menginterpolasi agregat orde nol secara berurutan ke agregat orde -1, -2, dan seterusnya. Pada tahap pertama, kami mengganti setiap agregat orde nol dengan salinan agregat orde pertama, dikurangi dengan a rasio 1/7, dan seterusnya. Dengan konstruksi ini, relasi tersebut tetap berlaku untuk nilai-nilai yang semakin kecil. Setelah ekstra dan interpolasi tanpa akhir, kita memperoleh himpunan dimensi yang serupa dengan diri kita sendiri .

Selain itu, dimensi suatu benda dalam ruang 3 tidak serta merta mengharuskannya berupa garis lurus atau kurva lain yang dapat diluruskan. Dia bahkan tidak harus koheren. Setiap dimensi kompatibel dengan dimensi topologi yang lebih kecil atau sama. Secara khusus, dimensi topologi alam semesta Fournier, yang tak terbatas di kedua arah, sama dengan 0, karena ia merupakan “debu” yang sepenuhnya terputus.

DISTRIBUSI MASSA: HOMOGENEITAS FRAKTAL

Bagi saya, langkah dari geometri ke distribusi massa tampak sejelas mungkin. Jika setiap agregat bintang berorde nol dibebani dengan satuan massa, maka massa di dalam bola berjari-jari sama dengan nilainya , dan oleh karena itu . Selain itu, untuk memperoleh agregat berorde -1 dari agregat berorde nol, perlu untuk memecah sebuah bola yang kita anggap homogen dan menemukan bahwa bola tersebut terdiri dari tujuh bola yang lebih kecil. Pada tahap ini, aturan tersebut juga berlaku untuk jari-jari yang lebih kecil dari satu.

Mengingat distribusi massa yang dihasilkan di seluruh ruang 3, kita melihat bahwa ia sangat tidak homogen, meskipun pada fraktal Fournier homogenitasnya tidak ada bandingannya. (Ingat Gambar 120.) Secara khusus, dua bagian alam semesta Fournier yang identik secara geometris mengandung massa yang sama. Saya mengusulkan untuk menyebut distribusi massa ini homogen secara fraktal.

< Предыдущее определение сформулировано в терминах масштабно-инвариантных фракталов, но концепция фрактальной гомогенности в общем случае гораздо шире. Она применима к любому фракталу, для которого положительна и конечна хаусдорфова мера в размерности . Фрактальная гомогенность требует, чтобы масса, содержащаяся в множестве, была пропорциональна хаусдорфовой мере этого множества.

ALAM SEMESTA FOURNIER SEPERTI DEBU CANTOR. EKSPANSI D0

Saya harap pembaca tidak bingung dengan penggunaan terminologi fraktal yang ceroboh di bagian pembuka bab ini. Jelas sekali bahwa Fournier, tanpa menyadarinya, mengikuti jalan yang sejajar dengan jalan yang ditempuh oleh Penyanyi sezamannya. Perbedaan utamanya adalah konstruksi Fournier tertanam dalam ruang, bukan dalam interval garis. Untuk lebih meningkatkan kesamaan, cukup mengganti agregat Fournier berbentuk bola dengan balok (kubus berisi). Setiap agregat orde nol menjadi sebuah balok yang panjang sisinya 1, dan mencakup 7 agregat kecil dengan sisi 1/7: pusat salah satunya berimpit dengan pusat kubus asal, dan enam agregat lainnya menyentuh sub pusat. -kotak pada muka kubus asal.

Di bawah ini kita akan melihat bagaimana Fournier memperoleh makna dari fenomena fisika fundamental, dan bagaimana Hoyle sampai pada hasil yang sama. Dari sudut pandang geometris, kasusnya istimewa, meskipun di seluruh konstruksi kami menganut bentuk dan nilai segi delapan. Karena bola-bola tersebut tidak saling tumpang tindih, maka nilainya dapat berupa nilai apa pun yang berkisar dari 3 hingga tak terhingga, yang menghasilkan hukum di mana selama seluruh interval dari 0 hingga .

MODEL CHARLIER DAN ALAM SEMESTA FRAKTAL LAINNYA

Konstruksi di atas tidak menghindari kekurangan apa pun yang menjadi ciri model fraktal pertama. Yang paling mencolok adalah model Fournier, seperti model kurva Koch di Bab 6 dan model debu Cantor di Bab 8, ternyata benar sekali. Untuk memperbaiki situasi, Charlier mengusulkan untuk memberikan kemampuan untuk berpindah dari satu tingkat hierarki ke tingkat hierarki lainnya, mengambil nilai dan .

Reputasi Charlier di kalangan ilmiah begitu tinggi sehingga, terlepas dari semua pujiannya yang murah hati terhadap Fournier, yang diungkapkan dalam semua bahasa sains terkemuka pada saat itu, bahkan model aslinya segera dikaitkan dengan penerjemah terkenal, dan bukan kepada siapa pun. . penulis terkenal. Model baru ini banyak dibicarakan pada saat itu, terutama di tahun . Terlebih lagi, hal ini menarik perhatian Emile Borel yang sangat berpengaruh, yang komentarnya sangat mendalam, meski agak kering. Namun, sejak saat itu, kecuali beberapa upaya keras untuk mengungkapnya, model Charlier telah terlupakan (alasan yang tidak terlalu meyakinkan atas terlupakannya hal tersebut dijelaskan dalam, hal. 20-22 dan 408-409). Namun, dia dengan keras kepala menolak untuk mati. Gagasan utama telah ditemukan berkali-kali oleh peneliti yang berbeda secara independen satu sama lain; Saya terutama merekomendasikan untuk melihatnya. (Lihat juga bagian PAUL LEVY di Bab 40.) Namun, yang menurut saya paling penting adalah bahwa dasar fraktal alam semesta Fournier tersirat dalam pembahasan turbulensi dan galaksi dalam karya tersebut (lihat Bab 10) dan dalam model galaksi. genesis, diusulkan oleh Hoyle (kami akan mempertimbangkannya di bawah).

Komponen fraktal utama juga terdapat dalam model saya (lihat bab 32 hingga 35).

Dalam hal ini, timbul pertanyaan: mungkinkah pola distribusi galaksi tidak berupa fraktal dengan satu atau dua ambang batas? Saya pikir tidak. Jika kita setuju bahwa distribusinya harus invarian skala (alasannya diuraikan dalam Bab 11), dan bahwa himpunan tempat materi terkonsentrasi bukanlah himpunan skala standar, kita tidak punya pilihan selain menerima fraktalitas himpunan ini. .

Mengingat pentingnya invariansi skala, tidak sulit untuk memahami mengapa generalisasi model Fournier bebas skala Charlier gagal sejak awal.< Оно, кстати, позволяет величине bervariasi tergantung pada itu dalam dua batas, dan . Berikut topik diskusi lainnya: dimensi efektif tidak harus memiliki satu nilai tunggal, nilai ini dapat mengambang di antara batas atas dan bawah. Kami akan kembali ke topik ini di Bab 15.

MENGAPA FOURNIER MENGHARAPKAND= 1?

Sekarang mari kita bahas argumentasi yang sangat mengesankan yang mengarahkan Fournier pada kesimpulan bahwa indikatornya harus sama dengan 1 (lihat, hal. 103). Argumen ini sendiri merupakan argumen serius yang mendukung kita untuk tidak melupakan nama penulisnya.

Mari kita perhatikan kumpulan galaksi dengan tatanan sembarang yang bermassa dan berjari-jari. Menghilangkan keraguan yang sia-sia dan menerapkan rumus benda dengan simetri bola pada kasus ini, mari kita asumsikan bahwa potensial gravitasi pada permukaan bola sama dengan ( - konstanta gravitasi). Sebuah bintang yang jatuh di alam semesta kita bertabrakan dengan permukaannya dengan kecepatan tinggi .

Menurut Fournier, kesimpulan yang sangat penting dapat diambil dari fakta bahwa tidak ada bintang yang dapat diamati bergerak dengan kecepatan melebihi 1/300 kecepatan cahaya. Massa yang terkandung di dalam bola dunia bertambah berbanding lurus dengan jari-jarinya, bukan volumenya, atau dengan kata lain massa jenis materi di dalam bola dunia berbanding terbalik dengan luas permukaannya... Mari kita jelaskan yang terakhir pernyataan - potensial pada permukaan bola selalu sama, karena berbanding lurus dengan massa materi di dalam bola dan berbanding terbalik dengan jarak dari pusat. Akibatnya, kecepatan bintang yang mendekati kecepatan cahaya jarang terjadi di bagian mana pun di Alam Semesta.

MEMOTONG HOYLE; KRITERIA JEANS

Distribusi hierarki juga muncul dalam teori Hoyle (lihat), yang menyatakan bahwa galaksi dan bintang terbentuk melalui proses kaskade, dan proses ini dimulai dengan gas homogen.

Mari kita perhatikan awan gas bermassa, dipanaskan sampai suhu tertentu dan didistribusikan dengan kepadatan seragam di dalam bola berjari-jari. Seperti yang ditunjukkan Gine, kapan situasi “kritis” muncul. (Ini adalah konstanta Boltzmann, a adalah koefisien numerik.) Karena berada dalam keadaan kritis, awan gas primer tidak stabil dan pasti menyusut.

Hoyle mendalilkan bahwa (a) besarnya mencapai nilai kritis pada suatu titik di awal, (b) kompresi berhenti ketika volume awan gas berkurang menjadi 1/25 dari volume aslinya, dan (c) setiap awan pada tahap ini pecah menjadi lima awan yang lebih kecil dengan ukuran yang sama, massa dan jari-jari. Artinya, proses kembali ke tempat yang sama di mana ia dimulai: hasilnya adalah keadaan tidak stabil, diikuti oleh tahap kompresi dan pemisahan yang kedua, lalu yang ketiga, dan seterusnya. Keruntuhan berhenti hanya ketika awan menjadi sangat buram sehingga tetap bertahan. yang dihasilkan Ketika gas dikompresi, ada panas di dalamnya.

Seperti di berbagai area lain di mana proses kaskade serupa terjadi, saya mengusulkan untuk menerapkan terminologi umum untuk kasus ini, yaitu, kita akan menyebut lima awan dadih, dan proses kaskade itu sendiri - mengental. Seperti yang saya sebutkan saat memperkenalkan istilah terakhir, saya tidak bisa menahan sindiran terhadap galaksi.

Demi kemudahan dalam merepresentasikan modelnya secara grafis, Fournier memperkenalkan , sementara Hoyle mengklaim bahwa nilainya dapat dibenarkan secara fisik. Perincian ilustrasi geometris Fournier melampaui batas wajar atau perlu. Pernyataan Hoyle mengenai struktur spasial keju cottage, sebaliknya, agak kabur. Kita harus menunggu hingga Bab 23, di mana kita melihat pelipatan acak, untuk implementasi model Hoyle secara mendetail. Meskipun demikian, perbedaan yang disebutkan di atas bukanlah hal yang sangat penting: hal yang utama adalah fakta bahwa, yaitu, indikator harus menjadi bagian integral dari konstruksi kita jika kita ingin penggumpalan berakhir pada kondisi yang sama dengan awal mulanya. , - dan khususnya, ketidakstabilan Jeans.

Selain itu, jika durasi tahap pertama diambil 1, maka menurut data dinamika gas, durasi tahap tersebut adalah . Akibatnya, total durasi seluruh proses, yang terdiri dari tahapan yang tak terhingga jumlahnya, tidak melebihi 1,2500.

EKUIVALENSI PENDEKATAN FOURNIER DAN HOYLE TERHADAP KESIMPULAND= 1

Pada batas awan gas tidak stabil yang memenuhi kriteria Jeans, kecepatan dan suhu dihubungkan oleh hubungan , karena keduanya sama dengan (Fournier) dan (Gene). Sekarang mari kita ingat bahwa dalam termodinamika statistik, suhu suatu gas berbanding lurus dengan akar rata-rata-kuadrat kecepatan molekul-molekulnya. Artinya, dari gabungan kriteria Fournier dan Jeans dapat diasumsikan bahwa pada batas awan kecepatan jatuhnya suatu benda makroskopis berbanding lurus. kecepatan rata-rata molekulnya. Analisis yang cermat terhadap peran suhu dalam kriteria Jeans tentu akan menunjukkan bahwa kedua kriteria ini setara.< Вероятнее всего, аналогия распространяется и на справедливость отношения внутри галактик, о чем сообщает Валленквист в .

MENGAPAD= 1,23, DAN BUKAND= 1?

Kesenjangan antara makna empirik dan makna teoritis memunculkan Fournier dan Hoyle masalah penting. P. J. E. Peebles menelitinya pada tahun 1974 dari perspektif teori relativitas. Dalam karyanya, aspek fisik dan statistik (tetapi bukan geometris) dari masalah tersebut mendapat liputan yang luas.

DIMENSI FRAKTAL LANGIT

Langit adalah proyeksi Alam Semesta. Untuk mendapatkan proyeksi ini, setiap titik di Alam Semesta dideskripsikan terlebih dahulu dengan koordinat bola , dan , lalu koordinatnya diganti dengan 1. Jika Alam Semesta adalah fraktal berdimensi , dan asal muasal sistem referensinya adalah milik Alam Semesta ini ( lihat Bab 22), maka struktur proyeksi, sebagai suatu peraturan, ditentukan oleh alternatif berikut: menyiratkan bahwa proyeksi tersebut mencakup area langit yang tidak nol, sedangkan proyeksi itu sendiri memiliki dimensi fraktal .< Как показано на рис. 141 и 143, «правило» не лишено исключений, обусловленных структурой фрактала и/или/ выбором точки отсчета. О таких правилах часто говорят «истинно с вероятностью 1».

CATATAN TENTANG EFEK LANGIT TERBAKAR (SALAH DISEBUT PARADOX OLBERS)

Aturan dari bagian sebelumnya sangat berkaitan dengan motivasi yang mengarahkan berbagai peneliti (termasuk Fournier) untuk menemukan alam semesta fraktal versi mereka sendiri. Mereka memahami bahwa alam semesta seperti itu secara geometris “membatalkan” efek langit yang terbakar, yang juga sering (tetapi salah) disebut paradoks Olbers. Jika kita berasumsi bahwa sebaran benda langit adalah seragam (yaitu, pada semua skala), maka langit di atas kita seharusnya mendapat penerangan yang hampir seragam baik pada malam hari maupun siang hari, dan kecerahan penerangan ini harus sebanding dengan matahari. .

Paradoks ini tidak lagi menarik perhatian para fisikawan, karena telah dibatalkan oleh teori relativitas, teori alam semesta yang mengembang, dan pertimbangan lainnya. Namun, kematiannya memiliki efek samping yang menarik: banyak komentator mulai mengutip penjelasan favorit mereka tentang efek langit yang menyala-nyala - beberapa dengan harapan dapat membenarkan penghinaan mereka terhadap pengelompokan, sementara yang lain, sebaliknya, sepenuhnya menyangkal kenyataan tersebut. Sudut pandang yang sangat aneh, harus saya katakan. Sekalipun kita berasumsi bahwa pengelompokan galaksi tidak ada hubungannya dengan tidak adanya efek langit yang terbakar, hal ini tetap ada dan memerlukan studi yang tepat. Terlebih lagi, seperti yang akan kita lihat di Bab 32, konsep alam semesta yang mengembang tidak hanya kompatibel dengan homogenitas standar, namun juga dengan homogenitas fraktal.

Efek dari langit yang terik dapat dijelaskan dengan sangat sederhana. Karena jumlah cahaya yang dipancarkan suatu bintang berbanding lurus dengan luas permukaannya, maka jumlah cahaya yang sampai ke pengamat yang berada jauh dari bintang haruslah , tetapi luas permukaan tampak bintang juga harus . Jadi, perbandingan jumlah cahaya terhadap sudut bola semu tidak bergantung pada . Selain itu, jika sebaran bintang di Alam Semesta seragam, maka hampir semua arah yang Anda lihat cepat atau lambat akan bertemu dengan bintang tertentu. Akibatnya, langit diterangi cahaya bintang secara merata dan tampak bercahaya. (Cakram bulan dalam hal ini membentuk wilayah yang sangat gelap - setidaknya tanpa adanya difusi atmosfer.)

Jika kita berasumsi bahwa Alam Semesta adalah fraktal dan dimensinya adalah , maka paradoksnya akan teratasi dengan sendirinya. Dalam hal ini, proyeksi Alam Semesta ke cakrawala merupakan himpunan fraktal yang berdimensi sama, yaitu himpunan luas nol. Bahkan jika bintang-bintang memiliki radius bukan nol, sebagian besar arahnya menuju tak terhingga tanpa bertemu satu bintang pun di jalurnya. Jika kita melihat ke arah tersebut, yang kita lihat hanyalah gelapnya langit malam. Jika interval di mana , diikuti oleh interval di mana , maka latar belakang langit tidak akan sepenuhnya hitam, namun pencahayaannya sangat redup.

Kepler menarik perhatian pada efek langit yang terbakar tak lama setelah Galileo, dalam “Pesan Bintangnya,” memuji gagasan Alam Semesta tanpa batas. Dalam “Conversation with the Starry Messenger” (1610), Kepler mengajukan keberatan berikut: “Anda tidak ragu sama sekali untuk menyatakan bahwa lebih dari 10.000 bintang terlihat untuk dilihat... Jika memang demikian, dan jika [bintang-bintang ] memiliki sifat yang sama dengan Matahari kita, lalu mengapa semua matahari ini tidak secara kolektif melebihi kecerahan Matahari kita?... Mungkinkah mereka terhalang oleh eter? Tidak sedikit pun... Jelas sekali bahwa dunia kita sama sekali tidak bisa menjadi bagian dari sekumpulan dunia lain yang tak terhitung banyaknya” (lihat, hal. 34-35).

Kesimpulannya cukup kontroversial, namun argumentasinya tidak dilupakan - buktinya adalah pernyataan Edmund Halley (yang dibuatnya pada tahun 1720): “Saya pernah mendengar keberatan lain, yang mengatakan bahwa jika jumlah bintang tetap lebih dari terbatas, maka seluruh lengkungan bola terlihat mereka akan diterangi sepenuhnya.” Keberatan ini kemudian dibahas oleh de Chezo dan I. G. Lambert, tetapi penulisnya tetap dikaitkan teman baik Gauss kepada astronom Jerman Olbers. Istilah "paradoks Olbers", yang sejak itu digunakan untuk menggambarkan kontradiksi ini, merupakan sebuah skandal namun bersifat gejala. Hasil observasi yang termasuk dalam kategori “tidak tunduk pada klasifikasi” (lihat hal. 51) sering kali dikaitkan dengan perwakilan pertama dari Mayoritas Resmi, yang akan menghiasinya dengan pembungkus yang sepenuhnya dapat diklasifikasikan, meskipun hanya sementara. Pembahasan subjek dalam perspektif sejarah dapat ditemukan di.

CATATAN TENTANG GRAVITASI NEWTONIAN

Pendeta Bentley terus mengganggu Newton dengan satu pengamatan yang berkaitan erat dengan efek langit terbakar: jika distribusi bintang-bintang seragam, maka gaya yang mereka gunakan terhadap satu sama lain tidak terbatas. Kita dapat menambahkan bahwa potensi gravitasinya juga tidak terbatas. Dan distribusi apa pun yang , akan memberikan potensi tak terhingga dalam semua kasus kecuali . Teori potensial modern (teori Frostman) menegaskan fakta bahwa ada hubungan khusus antara gravitasi Newton dan nilai. Indikator yang diperoleh Fournier dan Hoyle juga harus dikaitkan dengan manifestasi hubungan ini.< Положение Фурнье о том, что «гравитационный потенциал на поверхности сферы всегда одинаков», является центральным в teori modern potensi. " Kuadrat rasio kecepatan yang didalilkan Fournier tepat berada di tengah-tengah interval tersebut.

SEMESTA Fraktal AGLUTINASI?

Banyak peneliti percaya bahwa pembentukan bintang-bintang dan benda-benda langit lainnya dapat dijelaskan oleh aliran ke atas (yaitu, aglutinasi bertahap dari partikel-partikel debu yang sangat tersebar menjadi bongkahan-bongkahan yang semakin besar), tanpa ingin mendengar apa pun tentang aliran menurun a 1a Hoyle (yaitu , fragmentasi bertahap dari massa yang sangat besar dan tersebar menjadi bagian-bagian yang lebih kecil).

Alternatif serupa muncul sehubungan dengan kaskade yang didalilkan dalam teori turbulensi (lihat Bab 10). Aliran Richardson mengalir ke bawah menuju pusaran yang semakin kecil, namun aliran ke atas juga dapat berpartisipasi dalam proses tersebut (lihat Bab 40, bagian LEWIS FRY RICHARDSON). Dengan demikian, hubungan antara kaskade ke bawah dan ke atas diharapkan dapat segera dijelaskan dengan baik.

ARRAY FRAKTAL TELESKOP

Hampir tidak ada sentuhan akhir yang lebih tepat dalam diskusi ini selain pernyataan mengenai instrumen yang digunakan untuk mengamati galaksi. Untuk meningkatkan kualitas pengamatan, Dyson mengusulkan penggantian teleskop tunggal berukuran besar dengan teleskop kecil. Diameter masing-masing teleskop kecil harus sekitar 0,1 m (ukuran gangguan atmosfer terkecil yang signifikan secara optik), pusatnya harus membentuk pola hierarki fraktal, dan koneksi antar teleskop akan disediakan oleh interferometer Curry. Analisis kasar mengarah pada kesimpulan bahwa sebagai nilai yang sesuai dimensi harus diambil 2/3. Inilah kesimpulan Dyson sendiri: “Rangkaian tiga kilometer yang terdiri dari 1024 teleskop sepuluh sentimeter yang dihubungkan oleh 1023 interferometer bukanlah usulan yang paling praktis saat ini. [Saya mengajukannya] sebagai ide teoritis untuk menunjukkan apa yang pada prinsipnya dapat dilakukan di sini.”

TINJAUAN MODEL FRAKTAL ACAK KLUSTER GALAKSI

Jika kita yakin bahwa kita dapat mendeskripsikan sebaran galaksi secara efektif menggunakan model fraktal yang ditemukan secara acak dan tidak kompleks maupun universal, maka tidak mengherankan jika model fraktal acak yang disengaja dapat memberi kita lebih banyak informasi. deskripsi yang efektif. Pertama-tama, kita dapat memahami pelipatan Hoyle dengan lebih baik dengan mempertimbangkannya dalam lingkungan yang tepat, yaitu di antara fraktal acak (lihat Bab 23). Menurut pendapat saya, yang lebih penting lagi adalah model acak yang saya kembangkan, yang akan kita bahas pada Bab 32 hingga 35. Salah satu argumen yang mendukung pertimbangan beberapa model adalah bahwa meningkatkan kualitas deskripsi harus mengorbankan peningkatan kualitas deskripsi. kompleksitas. Argumen kedua adalah bahwa setiap model dibangun di atas debu fraktal khusus, yang masing-masing memerlukan pertimbangan terpisah. Mari kita pertimbangkan secara singkat model-model ini dalam urutan yang logis.

Sekitar tahun 1965, saya mulai memberikan hubungan tersebut dengan model yang sesuai di mana “pusat alam semesta” tidak ada sebagai sebuah konsep. Saya pertama kali mencapai tujuan ini dengan menggunakan model jalan acak yang dijelaskan dalam Bab 32. Kemudian, sebagai alternatif, saya mengembangkan model trem, yang intinya adalah bahwa sekumpulan trem tertentu yang saling independen dan ditempatkan secara acak dengan radius acak dipotong. ruang, dan batas atas jari-jarinya dapat mencapai ambang batas atas, yang bisa terbatas atau tidak terbatas.

Karena kedua model dipilih semata-mata karena alasan kesederhanaan formal, saya sangat terkejut dengan nilai prediktifnya. Fungsi korelasi teoritis saya ternyata sesuai dengan fungsi kurva yang diberikan oleh Peebles (lihat, hal. 243-249).< Точнее, два моих приближения совпали на двухточечной корреляции, случайные блуждания дали хорошую трех- и плохую четырехточечную корреляции, а сферические тремы оказались на высоте во всех известных корреляциях.

Sayangnya, contoh yang dihasilkan oleh model ini terlihat sangat tidak realistis. Dengan menggunakan konsep yang saya kembangkan khusus untuk tujuan ini, yang akan saya bahas di Bab 35, model awal saya menunjukkan sifat lacunar yang tidak dapat diterima. Dalam kasus model trem, kekurangan ini dapat diperbaiki dengan memperkenalkan bentuk trem yang lebih kompleks. Untuk model jalan acak, saya menggunakan “subordinator” yang tidak terlalu lacunar.

Dengan demikian, studi tentang gugus galaksi telah mendorong perkembangan geometri fraktal secara signifikan. Saat ini, cakupan penerapan geometri fraktal dalam studi gugus galaksi telah berkembang secara signifikan, jauh melampaui penerapan tersebut pembersihan umum dan debugging yang telah kita lakukan di bab ini.

POTONG BERLIAN SEPERTI BINTANG

Sebaran endapan intan di kerak bumi sangat mirip dengan sebaran bintang dan galaksi di cakrawala. Bayangkan sebuah peta dunia yang besar, di mana setiap tambang berlian, setiap deposit kaya - sekarang sedang dikembangkan atau sudah ditinggalkan - ditandai dengan pin. Jika kita melihat peta dari jarak yang cukup jauh, kita akan melihat bahwa sebaran pin sangat tidak merata. Ada beberapa pin terisolasi yang tersebar di sana-sini, namun sebagian besar terkonsentrasi di beberapa area yang diberkati (atau terkutuk). Permukaan bumi di wilayah ini, pada gilirannya, sama sekali tidak dilapisi berlian secara merata. Melihat lebih dekat masing-masing area tersebut, kita kembali melihat bahwa sebagian besar area masih kosong, sementara beberapa sub-area yang tersebar menunjukkan peningkatan konsentrasi berlian secara signifikan. Proses ini dapat dilanjutkan dalam beberapa kali lipat.

Apakah Anda tergoda untuk menerapkan konsep curdling dalam konteks ini? Bagi saya, saya akan mengatakan bahwa model seperti itu ada, diusulkan oleh de Wis, dan kami akan mempertimbangkannya di Bab 39 di bagian FRAKTAL NON-LACUNARY.

Buku Fournier menawarkan penjelasan berikut untuk ilustrasi ini: “Multiverse, yang dibangun berdasarkan prinsip salib atau segi delapan, bukanlah rencana dunia kita, tetapi membantu menunjukkan kemungkinan keberadaan alam semesta serupa yang berurutan dalam jumlah tak terbatas. tanpa menimbulkan efek “langit terbakar”. Jumlah materi di setiap bola dunia berbanding lurus dengan jari-jarinya. Kondisi ini diperlukan untuk mematuhi hukum gravitasi dan radiasi. Di beberapa arah, langit tampak hitam pekat - meskipun jumlah alam semesta tidak terbatas. "Nomor dunia" di pada kasus ini adalah, tidak seperti di dunia nyata." alih-alih . Konstruksi dilanjutkan satu langkah lebih jauh dari yang mungkin dilakukan pada Gambar. 141.

Fraktal (Dinamis).

Fraktal jenis ini muncul ketika mempelajari sistem dinamis nonlinier (sesuai dengan namanya). Perilaku sistem seperti itu dapat dijelaskan dengan fungsi nonlinier kompleks (polinomial) f(z). Mari kita ambil titik awal z0 pada bidang kompleks. Sekarang perhatikan barisan bilangan tak terhingga pada bidang kompleks, yang masing-masing diperoleh dari bilangan sebelumnya: z0, z1 = f(z0), z2 = f(z1), ... zn+1 = f(zn). Bergantung pada titik awal z0, barisan tersebut dapat berperilaku berbeda: cenderung tak terhingga sebagai n → ∞; berkumpul ke suatu titik akhir; secara siklis mengambil serangkaian nilai tetap; Opsi yang lebih kompleks juga dimungkinkan.

Jadi, setiap titik z pada bidang kompleks memiliki perilakunya sendiri selama iterasi fungsi f(z), dan seluruh bidang dibagi menjadi beberapa bagian. Selain itu, titik-titik yang terletak pada batas-batas bagian-bagian ini memiliki sifat-sifat berikut: dengan perpindahan kecil yang sewenang-wenang, sifat perilakunya berubah secara tajam (titik-titik tersebut disebut titik bifurkasi). Jadi, ternyata himpunan titik yang mempunyai satu jenis perilaku tertentu, serta himpunan titik bifurkasi, sering kali mempunyai sifat fraktal. Ini adalah himpunan Julia untuk fungsi f(z).

Himpunan Mandelbrot dibangun agak berbeda. Perhatikan fungsi fc(z) = z2 + c, dimana c adalah bilangan kompleks. Mari kita buat barisan fungsi ini dengan z0 = 0; bergantung pada parameter c, fungsi tersebut dapat menyimpang hingga tak terhingga atau tetap terbatas. Selain itu, semua nilai c yang barisan ini dibatasi membentuk himpunan Mandelbrot. Ia dipelajari secara rinci oleh Mandelbrot sendiri dan ahli matematika lainnya, yang menemukan banyak sifat menarik dari himpunan ini.

Terlihat bahwa definisi himpunan Julia dan Mandelbrot serupa satu sama lain. Faktanya, kedua rangkaian ini berkaitan erat. Yaitu, himpunan Mandelbrot adalah semua nilai parameter kompleks c yang himpunan Julia fc(z) terhubung (suatu himpunan disebut terhubung jika tidak dapat dibagi menjadi dua bagian yang terpisah-pisah, dengan beberapa syarat tambahan).

Ini adalah kelompok fraktal terbesar. Mereka diperoleh dengan menggunakan proses nonlinier dalam ruang berdimensi n. Proses dua dimensi adalah yang paling banyak dipelajari. Ketika menafsirkan proses iteratif nonlinier sebagai sistem dinamis diskrit, terminologi teori sistem ini dapat digunakan: potret fase, proses keadaan tunak, penarik, dll.

Diketahui bahwa sistem dinamis nonlinier mempunyai beberapa keadaan stabil. Keadaan di mana sistem dinamis menemukan dirinya sendiri setelah sejumlah iterasi tertentu bergantung pada keadaan awalnya. Oleh karena itu, setiap keadaan stabil (atau, seperti yang mereka katakan, penarik) memiliki wilayah keadaan awal tertentu, yang darinya sistem tersebut akan masuk ke keadaan akhir yang sedang dipertimbangkan. Dengan demikian, ruang fase sistem dibagi menjadi area tarikan penarik. Jika ruang fasenya dua dimensi, maka warnai daerah tarik-menariknya warna yang berbeda, Anda dapat memperoleh potret fase warna dari sistem ini (proses berulang). Dengan mengubah algoritma pemilihan warna, Anda bisa mendapatkan pola fraktal yang kompleks dengan pola multiwarna yang aneh. Kejutan bagi ahli matematika adalah kemampuan untuk menghasilkan struktur non-trivial yang sangat kompleks menggunakan algoritma primitif.

Sebagai contoh, perhatikan himpunan Mandelbrot (lihat Gambar 3 dan Gambar 4). Algoritme konstruksinya cukup sederhana dan didasarkan pada ekspresi iteratif sederhana:

Z = Z[i] * Z[i] + C,

dimana Zi dan C adalah variabel kompleks. Iterasi dilakukan untuk setiap titik awal C dari wilayah persegi panjang atau persegi - bagian dari bidang kompleks. Proses iteratif berlanjut hingga Z[i] melampaui lingkaran berjari-jari 2 yang pusatnya terletak di titik (0,0), (artinya penarik sistem dinamik berada pada tak terhingga), atau setelah waktu yang cukup lama. iterasi dalam jumlah besar (misalnya 200-500) Z[i] akan konvergen ke suatu titik pada lingkaran. Bergantung pada jumlah iterasi selama Z[i] tetap berada di dalam lingkaran, Anda dapat mengatur warna titik C (jika Z[i] tetap berada di dalam lingkaran untuk jumlah iterasi yang cukup besar, proses iterasi berhenti dan raster ini titik dicat hitam) .

Algoritma di atas memberikan perkiraan terhadap apa yang disebut himpunan Mandelbrot. Himpunan Mandelbrot berisi titik-titik yang tidak mencapai tak terhingga selama jumlah iterasi yang tak terhingga (titik-titik yang berwarna hitam). Titik-titik yang termasuk dalam batas himpunan (di sinilah struktur kompleks muncul) menuju tak terhingga dalam jumlah iterasi yang terbatas, dan titik-titik yang berada di luar himpunan menjadi tak terhingga setelah beberapa iterasi (latar belakang putih).

Contoh fraktal aljabar:

Mandelbrot siap
Julia siap
Fraktal Halley
Fraktal Newton

- 213,50 Kb

KEMENTERIAN PENDIDIKAN, ILMU PENGETAHUAN, PEMUDA DAN OLAHRAGA UKRAINA

AKADEMI KONSTRUKSI DAN ARSITEKTUR NEGARA ODESSA

DEPARTEMEN FISIKA

ABSTRAK

Disiplin: “Ilmu Bahan Fisika”

Pada topik: "FRAKTAL"

Lengkap:

st.gr. ZPGS – 501 M

Zlunyaev E.A.

s/kn No.08070

Diperiksa:

Prof., Gerega A.N.

Odessa - 2013

FRAKTAL

Perkenalan

1. Apa itu fraktal

2. Fraktal klasik

2.1 Kepingan salju Koch

2.2 Serbet dan karpet Sierpinski

3. Sistem-L

4. Penerapan praktis fraktal

literatur

Perkenalan

Ketika kebanyakan orang menganggap geometri di alam hanya terbatas pada bangun-bangun sederhana seperti garis, lingkaran, potongan kerucut, poligon, bola, permukaan kuadrat, serta kombinasinya. Misalnya, apa yang lebih indah dari pernyataan bahwa planet-planet ada di dalam kita tata surya bergerak mengelilingi matahari dalam orbit elips?

Namun, banyak sistem alam yang begitu kompleks dan tidak beraturan sehingga hanya menggunakan objek geometri klasik yang sudah dikenal untuk memodelkannya tampaknya tidak ada harapan lagi. Bagaimana, misalnya, Anda dapat membuat model pegunungan atau mahkota pohon dalam geometri? Bagaimana menggambarkan keanekaragaman konfigurasi biologis yang kita amati di dunia tumbuhan dan hewan? Bayangkan rumitnya sistem peredaran darah, yang terdiri dari banyak kapiler dan pembuluh darah dan mengantarkan darah ke setiap sel tubuh manusia. Bayangkan betapa cerdiknya susunan paru-paru dan kuncupnya, mengingatkan struktur pohon dengan tajuk bercabang.

Dinamika sistem alam yang nyata bisa jadi rumit dan tidak teratur. Bagaimana pendekatan pemodelan air terjun yang mengalir atau proses turbulen yang menentukan cuaca?

Fraktal dan kekacauan matematika adalah alat yang cocok untuk mengeksplorasi pertanyaan-pertanyaan ini. Istilah fraktal mengacu pada beberapa konfigurasi geometris statis, seperti cuplikan air terjun. Chaos adalah istilah dinamis yang digunakan untuk menggambarkan fenomena yang mirip dengan perilaku cuaca yang bergejolak. Seringkali apa yang kita amati di alam menggugah kita dengan pengulangan pola yang sama tanpa henti, ditambah atau dikurangi sebanyak yang kita inginkan. Misalnya pohon mempunyai cabang. Di cabang-cabang ini ada cabang-cabang yang lebih kecil, dan seterusnya. Secara teoritis, elemen percabangan berulang tanpa batas, menjadi semakin kecil. Hal serupa juga terlihat ketika melihat foto daerah pegunungan. Coba perbesar sedikit pegunungannya - Anda akan melihat pegunungan itu lagi. Ini adalah bagaimana sifat kesamaan diri yang merupakan karakteristik fraktal memanifestasikan dirinya.

Banyak penelitian tentang fraktal menggunakan kesamaan diri sebagai properti penentu. Mengikuti Benoit Madelbrot, kami menerima pandangan bahwa fraktal harus didefinisikan dalam dimensi fraktal (fraksional). Dari sinilah asal kata fraktal (dari bahasa latin fractus - pecahan).

Konsep dimensi pecahan merupakan konsep kompleks yang disajikan dalam beberapa tahap. Garis lurus merupakan benda satu dimensi, sedangkan bidang merupakan benda dua dimensi. Jika Anda memutar garis lurus dan bidang dengan baik, Anda dapat meningkatkan dimensi konfigurasi yang dihasilkan; dalam hal ini, dimensi baru biasanya berbentuk pecahan dalam beberapa hal, yang harus kita perjelas. Hubungan antara dimensi pecahan dan kesamaan diri adalah bahwa dengan bantuan kemiripan diri dimungkinkan untuk membangun sekumpulan dimensi pecahan dengan cara yang paling sederhana. Bahkan dalam kasus fraktal yang jauh lebih kompleks, seperti batas himpunan Mandelbrot, yang tidak memiliki kesamaan diri murni, terdapat pengulangan bentuk dasar yang hampir lengkap dalam bentuk yang semakin tereduksi.

Apa itu fraktal

Fraktal telah dikenal selama hampir satu abad, dipelajari dengan baik dan memiliki banyak penerapan dalam kehidupan. Fenomena ini sangat berdasar ide sederhana: variasi bentuk yang tak ada habisnya dalam keindahan dan variasi dapat diperoleh dari desain yang relatif sederhana hanya dengan menggunakan dua operasi - penyalinan dan penskalaan.

Konsep ini tidak memiliki definisi yang tegas. Oleh karena itu, kata “fraktal” bukanlah istilah matematika. Ini biasanya merupakan nama yang diberikan kepada bangun geometri yang memenuhi satu atau lebih sifat berikut: mempunyai struktur kompleks pada perbesaran berapa pun; adalah (kira-kira) mirip dengan diri sendiri; memiliki dimensi pecahan Hausdorff (fraktal), yang lebih besar dari dimensi topologi; dapat dibangun dengan prosedur rekursif.

Pada pergantian abad ke-19 dan ke-20, studi tentang fraktal lebih bersifat episodik daripada sistematis, karena sebelumnya para ahli matematika terutama mempelajari objek-objek “baik” yang dapat dipelajari dengan menggunakan metode dan teori umum. Pada tahun 1872, matematikawan Jerman Karl Weierstrass membuat contoh fungsi kontinu yang tidak dapat terdiferensiasi. Namun konstruksinya sepenuhnya abstrak dan sulit dipahami. Oleh karena itu, pada tahun 1904, Helge von Koch dari Swedia menemukan kurva kontinu yang tidak memiliki garis singgung di mana pun, dan cukup mudah untuk digambar. Ternyata ia memiliki sifat fraktal. Salah satu varian dari kurva ini disebut “kepingan salju Koch”.

Ide kemiripan diri tokoh diambil oleh orang Prancis Paul Pierre Levy, mentor masa depan Benoit Mandelbrot. Pada tahun 1938, artikelnya “Kurva dan permukaan bidang dan spasial yang terdiri dari bagian-bagian yang serupa dengan keseluruhan” diterbitkan, yang menggambarkan fraktal lain - kurva Levy C. Semua fraktal yang tercantum di atas secara kondisional dapat diklasifikasikan sebagai satu kelas fraktal konstruktif (geometris). Kelas lainnya adalah fraktal dinamis (aljabar), yang mencakup himpunan Mandelbrot. Penelitian pertama ke arah ini dimulai pada awal abad ke-20 dan dikaitkan dengan nama matematikawan Perancis Gaston Julia dan Pierre Fatou. Pada tahun 1918, Julia menerbitkan karya setebal hampir dua ratus halaman tentang iterasi fungsi rasional kompleks, yang menggambarkan himpunan Julia - seluruh keluarga fraktal yang terkait erat dengan himpunan Mandelbrot. Karya ini dianugerahi penghargaan oleh Akademi Perancis, namun tidak memuat satu ilustrasi pun, sehingga tidak mungkin untuk mengapresiasi keindahan benda terbuka. Terlepas dari kenyataan bahwa karya ini membuat Julia terkenal di kalangan ahli matematika pada waktu itu, karya ini dengan cepat dilupakan.

Perhatian kembali terhadap karya Julia dan Fatou baru muncul setengah abad kemudian, dengan munculnya komputer: merekalah yang membuat kekayaan dan keindahan dunia fraktal terlihat. Lagi pula, Fatou tidak akan pernah bisa melihat gambar yang sekarang kita kenal sebagai gambar himpunan Mandelbrot, karena jumlah perhitungan yang diperlukan tidak dapat dilakukan dengan tangan. Orang pertama yang menggunakan komputer untuk hal ini adalah Benoit Mandelbrot.

Pada tahun 1982, buku Mandelbrot “Fractal Geometry of Nature” diterbitkan, di mana penulis mengumpulkan dan mensistematisasikan hampir semua informasi tentang fraktal yang tersedia pada saat itu dan menyajikannya dengan cara yang mudah dan dapat diakses. Mandelbrot memberikan penekanan utama dalam presentasinya bukan pada rumus berat dan konstruksi matematika, tetapi pada intuisi geometris pembaca. Berkat ilustrasi yang diperoleh dengan menggunakan komputer dan cerita sejarah, yang dengannya penulis dengan terampil mengencerkan komponen ilmiah monografi, buku tersebut menjadi buku terlaris, dan fraktal dikenal masyarakat umum. Keberhasilan mereka di kalangan non-matematika sebagian besar disebabkan oleh fakta bahwa, dengan bantuan mereka desain sederhana dan rumus-rumus yang bahkan dapat dipahami oleh seorang siswa sekolah menengah, gambar yang dihasilkan sungguh menakjubkan dalam kompleksitas dan keindahannya. Ketika komputer pribadi menjadi cukup kuat, bahkan seluruh arah seni muncul - lukisan fraktal, dan hampir semua pemilik komputer dapat melakukannya. Sekarang di Internet Anda dapat dengan mudah menemukan banyak situs yang membahas topik ini.

1.1. Fraktal geometris (konstruktif).

Fraktal jenis ini dibangun secara bertahap. Pertama, alasnya digambarkan. Kemudian beberapa bagian alasnya diganti dengan pecahan. Pada setiap tahap berikutnya, bagian-bagian dari gambar yang sudah dibangun, mirip dengan bagian alas yang diganti, diganti lagi dengan bagian yang diambil pada skala yang sesuai. Setiap kali skalanya berkurang. Ketika perubahan menjadi tidak terlihat secara visual, diyakini bahwa gambar yang dibangun mendekati sumur fraktal dan memberikan gambaran tentang bentuknya. Untuk mendapatkan fraktal itu sendiri, diperlukan tahapan yang tidak terbatas. Dengan mengubah basis dan fragmen, Anda bisa mendapatkan banyak fraktal geometris yang berbeda.

Fraktal geometris bagus karena, di satu sisi, merupakan subjek studi ilmiah yang cukup serius, dan di sisi lain, dapat "dilihat" - bahkan orang yang jauh dari matematika akan menemukan sesuatu di dalamnya. Kombinasi ini jarang terjadi dalam matematika modern, di mana semua objek didefinisikan menggunakan kata-kata dan simbol-simbol yang tidak jelas. Ternyata banyak fraktal geometris yang dapat digambar secara harfiah di selembar kertas kotak-kotak. Mari kita segera membuat reservasi bahwa semua gambar yang dihasilkan (termasuk yang ditampilkan di poster ini) hanyalah perkiraan terbatas dari fraktal yang pada dasarnya tak terbatas. Namun Anda selalu dapat menggambar perkiraan sedemikian rupa sehingga mata tidak akan membedakan detail yang sangat kecil dan imajinasi kita akan mampu membuat gambaran fraktal yang benar. Misalnya, dengan selembar kertas grafik yang cukup besar dan waktu luang, Anda dapat secara manual menggambar perkiraan karpet Sierpinski yang begitu akurat sehingga dari jarak beberapa meter mata telanjang akan melihatnya sebagai fraktal nyata. Komputer akan menghemat waktu dan kertas sekaligus meningkatkan akurasi gambar.

Kepingan Salju Koch

T-persegi; H-fraktal

Segitiga Sierpinski

Pohon Pythagoras

Kurva retribusi

1.2. Fraktal dinamis (aljabar).

Mandelbrot siap

Julia siap

Fraktal Halley

Fraktal Newton

2. Fraktal klasik

2.1 Kepingan salju Koch

Pada awal abad kedua puluh, ahli matematika mencari kurva yang tidak mempunyai garis singgung di titik mana pun. Artinya, kurva tersebut tiba-tiba berubah arahnya, dan dengan kecepatan yang sangat tinggi (turunannya sama dengan tak terhingga). Pencarian kurva-kurva ini bukan hanya disebabkan oleh minat kosong para ahli matematika. Faktanya pada awal abad ke-20 mekanika kuantum berkembang sangat pesat. Peneliti M. Brown membuat sketsa lintasan pergerakan partikel tersuspensi dalam air dan menjelaskan fenomena ini sebagai berikut: atom-atom cairan yang bergerak secara acak menyerang partikel tersuspensi dan dengan demikian menggerakkannya. Setelah penjelasan tentang gerak Brown, para ilmuwan dihadapkan pada tugas untuk menemukan kurva yang paling mendekati gerak partikel Brown. Untuk melakukan ini, kurva harus memenuhi sifat-sifat berikut: tidak bersinggungan di titik mana pun. Ahli matematika Koch mengusulkan salah satu kurva tersebut. Kami tidak akan menjelaskan aturan konstruksinya, tetapi hanya menyajikan gambarnya, yang darinya semuanya akan menjadi jelas (Gbr. 1.1.1).

Gambar 2.1.1. Kepingan Salju Koch.

Satu properti penting, yang dimiliki batas kepingan salju Koch - panjangnya tak terhingga. Hal ini mungkin tampak mengejutkan karena kita terbiasa menghadapi kurva yang tidak tentu saja analisis matematis. Biasanya kurva halus atau setidaknya kurva mulus sepotong-sepotong selalu memiliki panjang yang terbatas (yang dapat diverifikasi dengan integrasi). Mandelbrot, dalam hal ini, menerbitkan sejumlah karya menarik yang mengeksplorasi pertanyaan tentang pengukuran panjang garis pantai Inggris Raya. Sebagai model dia

Beras. 2.1.2. Konstruksi kepingan salju Koch.

menggunakan kurva fraktal, mengingatkan pada tepi kepingan salju, hanya saja kurva tersebut memperkenalkan elemen keacakan untuk memperhitungkan keacakan di alam. Hasilnya, ternyata kurva yang menggambarkan garis pantai itu panjangnya tak terhingga.

2.2 Serbet dan karpet Sierpinski

Contoh lain dari fraktal sederhana yang serupa adalah serbet Sierpinski (Gbr. 1.2.1), ditemukan oleh ahli matematika Polandia Waclaw Sierpinski pada tahun 1915. Istilah serbet sendiri milik Mandelbrot. Dalam metode konstruksi di bawah ini, kita memulai dengan wilayah tertentu dan secara berurutan menghilangkan subwilayah internal. Nanti kita akan mempertimbangkan metode lain, khususnya yang menggunakan sistem L, serta berdasarkan fungsi yang diulang.

Gambar 2.2.1. Serbet Sierpinski

Misalkan himpunan awal S0 adalah segitiga sama sisi dengan daerah yang dilingkupinya. Mari kita bagi S0 menjadi empat daerah segitiga yang lebih kecil, menghubungkan titik tengah sisi-sisi segitiga asal dengan segmen-segmen. Mari hilangkan bagian dalam area segitiga kecil di tengah. Sebut saja himpunan sisanya S1 (Gbr. 1.2.2). Kami kemudian mengulangi proses untuk masing-masing dari tiga segitiga kecil yang tersisa untuk mendapatkan perkiraan S2 berikutnya. Melanjutkan cara ini, kita memperoleh barisan himpunan bersarang Sn yang perpotongannya dibentuk oleh serbet S.

Beras. 2.2.2. Konstruksi serbet Sierpinski

Jelasnya, luas total bagian-bagian yang dibuang selama konstruksi sama persis dengan luas segitiga aslinya. Pada langkah pertama kami membuang ¼ area tersebut. Pada langkah selanjutnya, kita membuang tiga buah segitiga yang masing-masing luasnya sama dengan ¼ 2 luas segitiga aslinya. Dengan pertimbangan seperti ini, kami yakin bahwa total bagian dari kawasan yang dibuang adalah:

1/4 + 3*(1/42) + 32*(1/43) + … + 3n-1*(1/4n) + … .

Jumlah ini setara. Oleh karena itu, kita dapat menyatakan bahwa himpunan S yang tersisa, yaitu serbet, memiliki luas nol. Hal ini membuat S menjadi himpunan “sempurna”, dalam artian ia membagi komplemennya menjadi daerah segitiga yang jumlahnya tak terhingga, namun ketebalannya nol.

Uraian pekerjaan

Kupu-kupu tentu saja tidak tahu apa-apa tentang ular. Tapi burung pemburu kupu-kupu tahu tentang mereka. Burung yang tidak mengenali ular dengan baik lebih mungkin...

Jika octo dalam bahasa Latin berarti “delapan”, lalu mengapa satu oktaf berisi tujuh nada?

Satu oktaf adalah interval antara dua bunyi terdekat dengan nama yang sama: do dan do, re dan re, dll. Dari sudut pandang fisika, “kekerabatan” dari...

Mengapa orang penting disebut Agustus?

Pada tahun 27 SM. e. Kaisar Romawi Oktavianus menerima gelar Augustus, yang dalam bahasa Latin berarti “suci” (untuk menghormati sosok yang sama, omong-omong...

Apa yang mereka tulis di luar angkasa?

Sebuah lelucon terkenal berbunyi: “NASA menghabiskan beberapa juta dolar untuk mengembangkan pena khusus yang dapat menulis di luar angkasa....

Mengapa dasar kehidupan adalah karbon?

Sekitar 10 juta molekul organik (yaitu berbasis karbon) dan hanya sekitar 100 ribu molekul anorganik yang diketahui. Selain itu...

Mengapa lampu kuarsa berwarna biru?

Berbeda dengan kaca biasa, kuarsa mentransmisikan sinar ultraviolet. DI DALAM lampu kuarsa Sumber radiasi ultraviolet adalah pelepasan gas dalam uap merkuri. Dia...

Mengapa kadang hujan dan kadang gerimis?

Dengan perbedaan suhu yang besar, aliran udara ke atas yang kuat muncul di dalam awan. Berkat mereka, tetesan air dapat bertahan di udara untuk waktu yang lama dan...