1. Pernyataan dapat dibuktikan bahwa jika sistem koordinat persegi panjang OXYZ diberikan dalam ruang, maka persamaan derajat pertama dengan tiga tidak diketahui x,y,z perlu dan cukup mendefinisikan bidang tertentu relatif terhadap sistem ini R. Persamaan ini disebut umum persamaan bidang dan memiliki tampilan berikutnya:
A X+ B pada+ C z+ D= 0 (17)
(bandingkan dengan persamaan umum (15) garis lurus pada bidang, yang berikut ini pada z = 0) dan mendefinisikan bidang tersebut R, tegak lurus terhadap vektor (A,B,C).
Vektor - vektor normal bidang R.
Persamaan (17) ekuivalen dengan persamaan berikut.
2. Persamaan bidang yang melalui suatu titik tertentu M( x 0, kamu 0, z 0):
A( X- X 0) + B( pada-pada 0) + C( z-z 0) = 0.
3. Persamaan bidang dalam segmen-segmen
,
Di mana 
; 
; 
.
4. Persamaan bidang yang melewati tiga poin yang diberikan, tidak terletak pada baris yang sama, ditulis sebagai determinan
,
Di mana ( X 1 , kamu 1 , z 1), (X 2 , kamu 2 , z 2), (X 3 , kamu 3 , z 3) - koordinat titik-titik tertentu.
Sudut antara dua bidang didefinisikan sebagai sudut antara vektor-vektor normalnya N 1 dan N 2. Oleh karena itu kondisi bidang sejajar
R 1 dan R 2:
dan kondisi tegak lurus dua bidang:
A 1 A 2 + B 1 DI DALAM 2 + C 1 DENGAN 2 = 0 .
Contoh 29. Melalui intinya KE(1, -3, 2) gambarlah sebuah bidang yang sejajar dengan vektor
sebuah =(1, 2, -3) dan b =(2,-1,-1) .
Larutan. Biarkan M ( X, pada, z) – titik sembarang pada bidang yang diinginkan. Vektor
km = (X- 1, pada+ 3, z- 2) terletak pada bidang ini, dan vektornya A Dan B sejajar dengannya. Oleh karena itu, vektor km , a dan b adalah koplanar. Maka hasil kali campurannya sama dengan nol:
.
Jadi -(x –1) - (y + 3) – 5(z – 2) = 0 atau x+ 7kamu+ 5z+ 10 = 0. Ini adalah persamaan bidang yang diinginkan.
Jenis yang berbeda persamaan garis dalam ruang
Garis lurus dalam ruang dapat dinyatakan sebagai:
1) garis perpotongan dua bidang yang tidak berhimpitan dan tidak sejajar R 1 dan R 2:
;
2) persamaan garis yang melalui suatu titik tertentu M(X 0 , pada 0 , z 0) dalam arah yang ditentukan oleh vektor L = (m, n, hal):
,
yang disebut persamaan garis kanonik di ruang hampa;
3) persamaan garis lurus yang melalui dua titik tertentu M(X 1 , pada 1 , z 1)
Dan M(X 2 , kamu 2 , z 2):
;
4) persamaan parametrik:
.
Contoh 30. Ubah persamaan garis lurus menjadi bentuk kanonik dan parametrik
.
Larutan. Garis lurus didefinisikan sebagai garis perpotongan dua bidang. Vektor normal dari bidang-bidang ini N 1 = (3,1,-2) dan N 2 = (4,-7,-1) tegak lurus terhadap garis yang diinginkan, maka hasil kali vektornya [ N 1 , N 2 ] = L sejajar dengannya adalah vektor [ N 1 , N 2 ] (atau yang collinear apa pun) dapat diambil sebagai vektor arah L garis lurus yang diinginkan.
[N 1 , N 2 ] = 
.
Anggap saja sebagai L = 3Saya + J + 5k. Masih menemukan titik tertentu pada garis tertentu. Untuk ini kita masukkan, misalnya, z = 0. Kita dapatkan
.
Setelah memecahkan sistem ini, kami menemukannya X = 1, pada= - 2. Jadi intinya KE(1, -2, 0) termasuk dalam garis tertentu, dan persamaan kanoniknya berbentuk
1. Jenis-jenis persamaan garis lurus pada bidang
| Nama | Penamaan |
| Persamaan umum garis lurus pada bidang | Kapak + Bou + C = 0 tegak lurus vektor = (A, B) |
| Persamaan garis dalam segmen | Dimana a adalah koordinat titik potong garis dengan sumbu Ox, dan b adalah koordinat titik potong garis dengan sumbu Oy. |
| Persamaan garis normal | xcos j + ysin j - p = 0, p adalah panjang garis tegak lurus yang turun dari titik asal ke garis lurus, dan j adalah sudut yang dibentuk tegak lurus tersebut dengan arah positif sumbu Ox. |
| Persamaan garis lurus dengan kemiringan |
2. Masalah dasar pada garis lurus dalam ruang
| Tugas | Implementasinya |
| Persamaan garis yang melalui dua titik M 1 (x 1, y 1, z 1) dan M 2 (x 2, y 2, z 2), |
|
| Sudut antar garis lurus pada suatu bidang |
|
| Kondisi tegak lurus dan paralelisme garis | Dua garis sejajar jika k 1 = k 2. Dua garis tegak lurus jika |
| Jarak titik M(x 0, y 0) ke garis lurus Ah + Wu + C = 0 |
|
3. Jenis-jenis persamaan bidang dalam ruang
| Nama | Penamaan |
| Persamaan bidang umum | Ax + By + Cz + D = 0, dimana A, B, C adalah koordinat vektor |
| Persamaan bidang yang melalui suatu titik M 0 (x 0, y 0, z 0) adalah tegak lurus vektor ini(A, B, C) | A (x – x 0) + B (y – y 0) + C (z – z 0) = 0. |
| Persamaan bidang dalam segmen | Bilangan a, b, c masing-masing merupakan titik potong bidang dengan sumbu x, y, z. |
4. Permasalahan dasar pada pesawat di luar angkasa
| Tugas | Implementasinya |
| Persamaan bidang yang melalui tiga titik |
|
| Jarak titik M 0 (x 0, y 0, z 0) ke bidang Ах+Бу+Сz +D =0 |
|
| Sudut antar bidang |
|
| Syarat paralelisme dan tegak lurus bidang | Pesawat terbang tegak lurus Jika: . Pesawat terbang, paralel, Jika |
5. Jenis-jenis persamaan garis lurus dalam ruang
| Nama | Penamaan |
| Persamaan parametrik suatu garis | |
| Persamaan garis kanonik |
|
| Persamaan umum garis lurus dalam ruang |
|
, dimana (m, n, p) adalah vektor arah garis, dan M 0 (x 0, y 0, z 0) adalah titik yang dilalui garis tersebut.
, dimana vektor arahnya6. Soal-soal dasar garis lurus dalam ruang
| Tugas | Implementasinya |
| Persamaan garis lurus dalam ruang, melewati dua titik M 1 (x 1, y 1, z 1) dan M 2 (x 2, y 2, z 2) |
|
| Sudut antar garis lurus dalam ruang |
|
| Syarat paralelisme dan tegak lurus garis dalam ruang | garis sejajar jika garis-garisnya tegak lurus jika . |
7. Permasalahan dasar pada bidang dan garis dalam ruang
8. Kurva orde kedua
| Nama | Rumus | Interpretasi geometris |
| Elips |
|
|
| Lingkaran |
|
|
| Hiperbola |
|
|
|
|
||
| Parabola | pada 2 = 2piksel |
|
|
|
9. Permukaan orde kedua
| Nama | Rumus | Interpretasi geometris |
| bola |
|
|
| silinder elips |
|
|
| silinder hiperbolik |
|
|
| silinder parabola |
|
|
| kerucut |
|
|
| elipsoid |
|
|
| hiperboloid jalur tunggal |
| |
| hiperboloid dua lembar |
|
|
| paraboloid elips |
|
|
| hiperbolis paraboloid |
|
atau
Dalam modul ini, siswa harus mempelajari materi teori yang diajukan elemen pendidikan. (cm. Materi teori dalam matematika tingkat tinggi: materi pendidikan untuk seorang siswa. Bagian I. Disusun oleh: Kalukova O.M., Kosheleva N.N., Nikitina M.G., Pavlova E.S., Emelyanova S.G. - Togliatti: TSU, 2005 dan tambahan. literatur)
Tabel 7 menyajikan jadwal pembelajaran materi teori pada modul “Geometri Analitik”
Tabel 7
| pelatihan | materi teori |
|
| Pelajaran pendengaran | ||
| "Konsep persamaan garis pada bidang" | ||
| "Pesawat dan garis di luar angkasa" | Materi teori dengan topik “Elemen Teori Himpunan” |
|
| "Kurva orde kedua" | Materi teori dengan topik “Elemen Teori Graf” |
|
| "Permukaan urutan kedua" | Materi teori dengan topik " Nilai eigen matriks" |
|
Untuk pertanyaan apa pun, hubungi konsultan akademik dengan mengajukan pertanyaan di forum portal pendidikan.
Siswa juga harus membiasakan diri dengan tugas-tugas khas dan latihan modul untuk menyelesaikan versi IPD Anda (lihat Panduan untuk menyelesaikan masalah: alat bantu mengajar untuk siswa Bagian I. Disusun oleh: Nikitina M.G., Pavlova E.S., - Togliatti: TSU, 2008.)
Tabel 8 menunjukkan jadwal penelitian masalah praktis modul "Geometri Analitik"
Tabel 8
| pelatihan | Pelajaran praktis |
|
| Pelajaran pendengaran | pekerjaan mandiri |
|
| Menyelesaikan masalah dengan topik "Garis lurus pada bidang" | ||
| Menyelesaikan masalah dengan topik "Bidang dan garis dalam ruang" | Memecahkan masalah pada topik "Elemen teori himpunan" |
|
| Memecahkan masalah pada topik "Kurva orde kedua" | Menyelesaikan masalah dengan topik “Elemen Teori Graf” |
|
| Memecahkan masalah pada topik "Permukaan orde kedua" | Menyelesaikan masalah pada topik "Nilai Eigen suatu matriks" |
|
Untuk semua pertanyaan, hubungi konsultan akademik dengan mengajukan pertanyaan di forum portal pendidikan atau selama jam konsultasi individu (jadwal konsultasi individu disajikan di portal pendidikan).
Siswa harus menyelesaikan pilihannya pekerjaan rumah(lihat pekerjaan rumah individu untuk siswa yang belajar dalam teknologi 30/70. Bagian I. Disusun oleh: Kalukova O.M., Kosheleva N.N., Nikitina M.G., Pavlova E.S., Emelyanova S.G. ., - Togliatti: TSU, 2005).
Jadwal pelaksanaan disajikan IDZ pada Tabel 9.
Tabel 9
| Minggu pelatihan | |
| dari 1 hingga 4 tugas |
|
| dari 5 hingga 7 tugas |
|
| dari tugas 8 hingga 11 |
|
| 12.13 tugas |
Pada akhir minggu ke-12, serahkan IDD ke konsultan akademis dan terima izin masuk untuk pengujian di portal pendidikan
Pada minggu ketigabelas Selama pelatihan, mahasiswa menjalani pengujian modul yang dituangkan dalam jadwal.
Semua persamaan bidang yang dibahas pada paragraf berikut dapat diperoleh dari persamaan umum bidang, dan juga direduksi menjadi persamaan umum pesawat. Jadi, ketika berbicara tentang persamaan bidang, yang mereka maksud adalah persamaan umum bidang, kecuali dinyatakan lain.
Persamaan bidang dalam segmen.
Lihat persamaan bidang 
, dimana a, b dan c adalah bilangan real bukan nol disebut persamaan bidang dalam segmen.
Nama ini bukan suatu kebetulan. Nilai-nilai mutlak bilangan a, b, dan c sama dengan panjang segmen yang dipotong oleh bidang pada sumbu koordinat Ox, Oy, dan Oz, dihitung dari titik asal. Tanda bilangan a, b dan c menunjukkan ke arah mana (positif atau negatif) segmen tersebut harus diplot pada sumbu koordinat.
Misalnya, mari kita membangun sistem persegi panjang koordinat bidang Oxyz ditentukan oleh persamaan bidang dalam segmen 
. Caranya, tandai sebuah titik yang berjarak 5 satuan dari titik asal pada arah negatif sumbu absis, 4 satuan pada arah negatif sumbu ordinat, dan 4 satuan pada arah positif sumbu aplikasi. Yang tersisa hanyalah menghubungkan titik-titik ini dengan garis lurus. Bidang segitiga yang dihasilkan adalah bidang yang bersesuaian dengan persamaan bidang dalam segmen-segmen bentuknya .
Untuk mendapatkan lebih banyak informasi lengkap simak artikel persamaan bidang dalam ruas-ruas, yang menunjukkan pengurangan persamaan bidang dalam ruas-ruas menjadi persamaan umum bidang, disana anda juga akan menemukan solusi terperinci contoh dan tugas yang khas.
Persamaan bidang normal.
Persamaan bidang umum bentuknya disebut persamaan bidang normal, Jika 
sama dengan satu, yaitu 
, Dan .
Anda sering melihat persamaan normal sebuah bidang ditulis sebagai . Berikut adalah cosinus arah dari vektor normal suatu bidang dengan satuan panjang tertentu, yaitu p adalah bilangan non-negatif yang sama dengan jarak dari titik asal ke bidang tersebut.
Persamaan normal bidang dalam sistem koordinat persegi panjang Oxyz mendefinisikan bidang yang dipindahkan dari titik asal sejauh p dalam arah positif dari vektor normal bidang tersebut 
. Jika p=0, maka bidang melewati titik asal.
Mari kita beri contoh persamaan bidang normal.
Biarkan bidang ditentukan dalam sistem koordinat persegi panjang Oxyz dengan persamaan umum bentuk bidang 
. Persamaan umum bidang ini merupakan persamaan normal bidang. Memang, vektor normal bidang ini adalah 
memiliki panjang sama dengan satu, Karena 
.
Persamaan bidang dalam bentuk normal memungkinkan Anda mencari jarak dari suatu titik ke bidang.
Kami menyarankan Anda memahami jenis persamaan bidang ini secara lebih rinci, melihat solusi rinci untuk contoh dan masalah yang umum, dan juga mempelajari cara mereduksi persamaan bidang umum menjadi tampak normal. Anda dapat melakukan ini dengan merujuk pada artikel tersebut.
Bibliografi.
- Atanasyan L.S., Butuzov V.F., Kadomtsev S.B., Kiseleva L.S., Poznyak E.G. Geometri. Buku teks untuk kelas 10-11 sekolah menengah.
- Bugrov Ya.S., Nikolsky S.M. Matematika yang lebih tinggi. Jilid satu: unsur aljabar linier dan geometri analitik.
- Ilyin V.A., Poznyak E.G. Geometri analitik.
12.1. Konsep dasar
Permukaan dan persamaannya
Suatu permukaan dalam ruang dapat dianggap sebagai tempat kedudukan titik-titik yang memenuhi suatu kondisi. Misalnya bola berjari-jari R yang berpusat di titik O 1 adalah tempat kedudukan geometri semua titik dalam ruang yang terletak pada jarak R dari titik O 1.
Sistem koordinat persegi panjang Oxyz di ruang angkasa memungkinkan kita membuat korespondensi satu-satu antara titik-titik dalam ruang dan tiga kali lipat bilangan x, y dan z - koordinatnya. Sifat persekutuan semua titik pada suatu permukaan dapat ditulis sebagai persamaan yang menghubungkan koordinat semua titik pada permukaan.
Persamaan suatu permukaan pada sistem koordinat persegi panjang Oxyz adalah persamaan F(x, y, z) = 0 dengan tiga variabel x, y dan z yang dipenuhi oleh koordinat setiap titik yang terletak di permukaan dan tidak dipenuhi koordinat titik, tidak berbaring di permukaan ini. Variabel x, y, dan z dalam persamaan permukaan disebut koordinat titik-titik permukaan saat ini.
Persamaan permukaan memungkinkan studi tentang sifat-sifat geometris suatu permukaan digantikan dengan studi tentang persamaannya. Jadi, untuk mengetahui apakah suatu titik M 1 (x 1 ;y 1 ;z 1) terletak pada suatu permukaan tertentu, cukup dengan memasukkan koordinat titik M 1 ke dalam persamaan permukaan, bukan variabel: jika koordinat ini memenuhi persamaan, maka titik terletak pada permukaan, jika tidak memenuhi maka tidak berbohong.
Persamaan bola
Mari kita cari persamaan bola berjari-jari R yang berpusat di titik O 1 (x 0 ;y 0 ;z 0). Menurut definisi bola, jarak setiap titiknya M(x; y; z) dari pusat O 1 (x 0 ;y 0 ;z 0) sama dengan jari-jari R, yaitu O 1 M= R. Tapi dimana. Karena itu,
Ini adalah persamaan bola yang diperlukan. Ia dipenuhi oleh koordinat titik mana pun dan tidak dipenuhi oleh koordinat titik yang tidak terletak pada bola tertentu.
Jika pusat bola Ο 1 berimpit dengan titik asal koordinat, maka persamaan bola berbentuk .
Jika persamaan berbentuk F(x;y;z) = 0 diberikan, maka, secara umum, persamaan tersebut mendefinisikan suatu permukaan tertentu dalam ruang.
Ungkapan “secara umum” berarti bahwa dalam beberapa kasus persamaan F(x; y; z) = 0 mungkin tidak mendefinisikan suatu permukaan, melainkan sebuah titik, garis, atau tidak mendefinisikan gambar geometris sama sekali. Mereka mengatakan “permukaannya merosot.”
Jadi, persamaan tersebut tidak dipenuhi oleh nilai riil apa pun dari x, y, z. Persamaan tersebut hanya dipenuhi oleh koordinat titik-titik yang terletak pada sumbu Ox (dari persamaan berikut: y = 0, z = 0, dan x adalah bilangan apa pun).
Jadi, suatu permukaan dalam ruang dapat didefinisikan secara geometris dan analitis. Hal ini mengarah pada perumusan dua tugas utama:
1. Suatu permukaan diberikan sebagai tempat kedudukan titik-titik. Temukan persamaan permukaan ini.
2. Diketahui persamaan F(x;y;z) = 0. Selidiki bentuk permukaan yang ditentukan oleh persamaan ini.
Persamaan garis dalam ruang
Garis dalam ruang dapat dianggap sebagai garis perpotongan dua permukaan (lihat Gambar 66) atau sebagai tempat kedudukan titik-titik yang sama pada dua permukaan.
Jika 
Dan 
- persamaan dua permukaan yang menentukan garis L, maka koordinat titik-titik garis tersebut memenuhi sistem dua persamaan dengan tiga hal yang tidak diketahui:
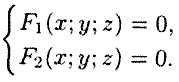(12.1)
Perbandingan sistem (12.1) disebut persamaan garis dalam ruang. Misalnya, ada persamaan untuk sumbu Ox.
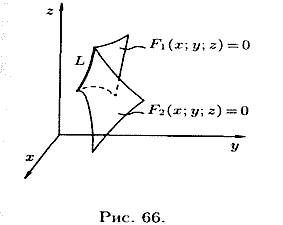
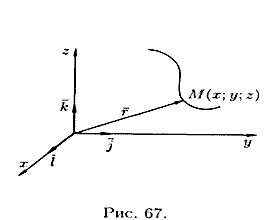
Garis dalam ruang dapat dianggap sebagai lintasan suatu titik (lihat Gambar 67). Dalam hal ini diberikan oleh persamaan vektor
atau persamaan parametrik
proyeksi vektor (12.2) pada sumbu koordinat.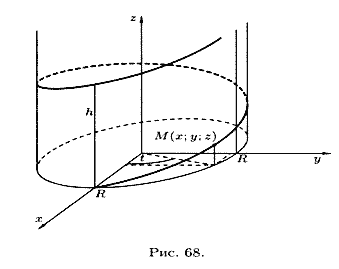 
Misalnya, persamaan parametrik heliks mempunyai bentuk
Jika titik M bergerak beraturan sepanjang generatrix silinder sirkular, dan silinder itu sendiri berputar beraturan terhadap sumbunya, maka titik M menggambarkan garis heliks (lihat Gambar 68).
12.2. Persamaan pesawat di luar angkasa
Permukaan paling sederhana adalah bidang. Bidang di ruang Oxyz dapat ditentukan cara yang berbeda. Masing-masing sesuai tipe tertentu persamaannya.
Persamaan bidang yang melewati suatu titik tertentu yang tegak lurus terhadap suatu vektor tertentu
Misalkan bidang Q di ruang Oxyz dibatasi oleh sebuah titik 
dan vektor tegak lurus terhadap bidang ini (lihat Gambar 69). Mari kita turunkan persamaan bidang Q. Ambil titik sembarang di atasnya dan buatlah sebuah vektor. Untuk setiap lokasi titik M pada bidang Q, vektor-vektornya dan saling tegak lurus, oleh karena itu vektor-vektor tersebut produk skalar sama dengan nol: , yaitu
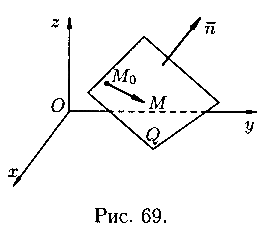(12.3)
Koordinat titik mana pun pada bidang Q memenuhi persamaan (12.3); koordinat titik-titik yang tidak terletak pada bidang Q tidak memenuhi persamaan ini (untuk titik tersebut ).
Persamaan (12.3) disebut persamaan bidang yang melalui suatu titik tertentu tegak lurus terhadap vektor. Ini adalah derajat pertama relatif terhadap koordinat saat ini x, y, z. Vektor tersebut disebut vektor normal bidang.
Memberikan koefisien A, B dan C pada persamaan (12.3) arti yang berbeda, Anda bisa mendapatkan persamaan bidang apa pun yang melalui titik tersebut. Himpunan bidang yang melalui suatu titik tertentu disebut kumpulan bidang, dan persamaan (12.3) disebut persamaan kumpulan bidang.
Persamaan bidang umum
Pertimbangkan persamaan umum tingkat pertama dengan tiga variabel x, y dan z:
Dengan asumsi setidaknya salah satu koefisien A, B, atau C tidak sama dengan nol, misalnya, kita menulis ulang persamaan (12.4) dalam bentuk
Membandingkan persamaan (12.5) dengan persamaan (12.3), kita melihat bahwa persamaan (12.4) dan (12.5) adalah persamaan bidang dengan vektor normal yang melalui titik tersebut. 
.
Jadi, persamaan (12.4) mendefinisikan bidang tertentu dalam sistem koordinat Oxyz. Persamaan (12.4) disebut persamaan umum bidang.
Kasus khusus persamaan bidang umum:
1. Jika D = 0, maka berbentuk . Persamaan ini terpenuhi pada intinya. Oleh karena itu, dalam hal ini pesawat melewati titik asal.
2. Jika C = 0, maka kita mempunyai persamaannya. Vektor normal tegak lurus terhadap sumbu Οz. Akibatnya, bidang tersebut sejajar dengan sumbu Οz; jika B = 0 - sejajar sumbu Oy, A = 0 - sejajar sumbu Ox.
3. Jika C = D = 0, maka bidang melewati sumbu sejajar sumbu Οz, yaitu bidang melewati sumbu Οz. Demikian pula, persamaan tersebut berhubungan dengan bidang yang masing-masing melewati sumbu Ox dan Oy.
4. Jika A = B = 0, maka persamaan (12.4) berbentuk , yaitu bidang tersebut sejajar dengan bidang Oxy. Demikian pula persamaan dan sesuai dengan bidang masing-masing sejajar dengan pesawat Oyz dan Οxz.
5. Jika A = B = D = 0, maka persamaan (12.4) berbentuk , yaitu z = 0. Ini adalah persamaan bidang Oxy. Demikian pula: y = 0 - persamaan bidang Οxz; x = O - persamaan bidang Oyz.
Persamaan bidang yang melalui tiga titik tertentu
Tiga titik dalam ruang yang tidak terletak pada garis lurus yang sama mendefinisikan suatu bidang tunggal. Mari kita cari persamaan bidang Q yang melalui tiga titik tertentu M 1 (x 1 ;y 1 ;z 1), M 2 (x 2 ;y 2 ;z 2) dan M 3 (x 3 ,y 3 ,z 3), tidak terletak pada satu garis lurus yang sama.
Mari kita ambil titik sembarang M(x;y;z) pada bidang dan menyusun vektor-vektornya , , . Vektor-vektor ini terletak pada bidang Q, oleh karena itu vektor-vektor tersebut koplanar. Kami menggunakan kondisi koplanaritas tiga vektor (produk campurannya sama dengan nol), kami memperoleh, mis.
(12.6)
Persamaan (12.6) adalah persamaan bidang yang melalui tiga titik tertentu.
Persamaan bidang dalam segmen
Biarkan pesawat memotong masing-masing segmen pada sumbu Ox, Oy dan Oz A, B Dan C, yaitu melewati tiga titik SEBUAH(sebuah;0;0), B(0;b;0) Dan C(0;0;c)(lihat Gambar 70). Substitusikan koordinat titik-titik ini ke dalam persamaan (12.6), kita peroleh
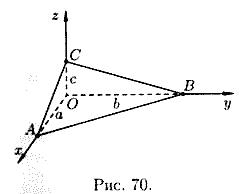
Memperluas determinannya, kita mempunyai , yaitu, atau
(12.7)
Persamaan (12.7) disebut persamaan bidang dalam segmen-segmen pada sumbunya. Lebih mudah digunakan saat membuat pesawat.
Persamaan bidang normal
Posisi bidang Q ditentukan sepenuhnya dengan menentukan vektor satuan yang arahnya tegak lurus OK, diturunkan ke
bidang dari titik asal, dan panjangnya P tegak lurus ini (lihat Gambar 71).
Biarkan OK = P, dan α, β, g adalah sudut yang dibentuk oleh vektor satuan е dengan sumbu Ox, Oy dan Οz. Kemudian . Mari kita ambil titik sembarang M(x; y; z) pada bidang dan menghubungkannya ke titik asal. Mari kita membentuk sebuah vektor. Untuk sembarang posisi titik M pada bidang Q, proyeksi vektor jari-jari ke arah vektor selalu sama dengan p :, yaitu atau
(12.8)
Persamaan (12.8) disebut persamaan normal bidang dalam bentuk vektor. Mengetahui koordinat vektor f dan e, kita menulis ulang persamaan (12.8) ke dalam bentuk
Persamaan (12.9) disebut persamaan normal bidang dalam bentuk koordinat.
Perhatikan bahwa persamaan umum bidang (12.4) dapat direduksi menjadi persamaan normal (12.9) dengan cara yang sama seperti yang dilakukan untuk persamaan garis pada bidang. Yaitu: kalikan kedua ruas persamaan (12.4) dengan faktor normalisasi 
, dimana tandanya diambil berlawanan dengan tanda suku bebas D persamaan umum bidang.
Pada bagian sebelumnya yang membahas bidang di ruang angkasa, kita mengkaji permasalahan ini dari perspektif geometri. Sekarang mari kita beralih ke mendeskripsikan bidang menggunakan persamaan. Melihat bidang dari sisi aljabar melibatkan pertimbangan jenis utama persamaan bidang dalam sistem koordinat persegi panjang O x y z ruang tiga dimensi.
Yandex.RTB RA-339285-1
Definisi persamaan bidang
Definisi 1Pesawat- Ini sosok geometris, terdiri dari poin individu. Setiap titik dalam ruang tiga dimensi berhubungan dengan koordinat yang ditentukan oleh tiga angka. Persamaan bidang menetapkan hubungan antara koordinat semua titik.
Persamaan bidang pada sistem koordinat persegi panjang 0xz berbentuk persamaan dengan tiga variabel x, y dan z. Koordinat titik mana pun yang terletak di dalam suatu bidang memenuhi persamaan tersebut, sedangkan koordinat titik lain yang terletak di luar bidang tertentu tidak memenuhi persamaan tersebut.
Mensubstitusikan suatu titik pada suatu bidang tertentu ke dalam persamaan bidang koordinat akan mengubah persamaan tersebut menjadi suatu identitas. Saat mengganti koordinat suatu titik yang terletak di luar bidang, persamaan tersebut berubah menjadi persamaan yang salah.
Persamaan bidang dapat memiliki beberapa jenis. Bergantung pada spesifik masalah yang dipecahkan, persamaan bidang dapat ditulis dengan berbagai cara.
Persamaan bidang umum
Mari kita rumuskan teoremanya lalu tuliskan persamaan bidangnya.
Teorema 1
Setiap bidang dalam sistem koordinat persegi panjang O x y z dalam ruang tiga dimensi dapat ditentukan dengan persamaan berbentuk A x + B y + C z + D = 0, di mana A, B, C dan D– beberapa bilangan real yang tidak sama dengan nol pada saat yang bersamaan. Persamaan apa pun yang berbentuk A x + B y + C z + D = 0 mendefinisikan bidang dalam ruang tiga dimensi
Persamaan bentuk A x + B y + C z + D = 0 disebut persamaan umum bidang. Jika Anda tidak melampirkan nomor A, B, C Dan D nilai tertentu, maka diperoleh persamaan bidang dalam bentuk umum.
Penting untuk dipahami bahwa persamaan λ · A x + λ · B y + λ · C z + λ · D = 0 akan mendefinisikan bidang dengan cara yang persis sama. Dalam persamaan tersebut, λ adalah bilangan real bukan nol. Artinya persamaan A x + B y + C z + D = 0 dan λ · A x + λ · B y + λ · C z + λ · D = 0 adalah ekuivalen.
Contoh 1
Persamaan umum bidang x - 2 · y + 3 · z - 7 = 0 dan - 2 · x + 4 · y - 2 3 · z + 14 = 0 dipenuhi oleh koordinat titik-titik yang sama yang terletak di tiga- ruang dimensi. Artinya keduanya mendefinisikan bidang yang sama.
Mari kita berikan penjelasan tentang teorema yang dibahas di atas. Sebuah bidang dan persamaannya tidak dapat dipisahkan, karena setiap persamaan A x + B y + C z + D = 0 berhubungan dengan bidang dalam sistem koordinat persegi panjang tertentu, dan setiap bidang yang terletak di ruang tiga dimensi berhubungan dengan persamaan bentuknya. A x + B y + C z + D = 0.
Persamaan bidang A x + B y + C z + D = 0 bisa lengkap atau tidak lengkap. Semua koefisien A, B, C dan D di persamaan lengkap berbeda dari nol. Jika tidak, persamaan umum bidang tersebut dianggap tidak lengkap.
Pesawat yang ditentukan persamaan yang tidak lengkap, dapat sejajar dengan sumbu koordinat, melalui sumbu koordinat, berimpit dengan bidang koordinat atau letaknya sejajar dengannya, melalui titik asal koordinat.
Contoh 2
Perhatikan posisi dalam ruang bidang yang diberikan oleh persamaan 4 · y - 5 · z + 1 = 0.
Letaknya sejajar dengan sumbu x dan terletak tegak lurus terhadap bidang O y z. Persamaan z = 0 mendefinisikan bidang koordinat O y z, dan persamaan umum bidang berbentuk 3 x - y + 2 z = 0 berhubungan dengan bidang yang melalui titik asal.
Klarifikasi penting: koefisien A, B dan C pada persamaan umum bidang mewakili koordinat vektor normal bidang.
Ketika mereka berbicara tentang persamaan sebuah bidang, yang mereka maksud adalah persamaan umum sebuah bidang. Semua jenis persamaan bidang yang akan kita bahas pada artikel selanjutnya diperoleh dari persamaan bidang umum.
Persamaan bidang normal
Persamaan bidang normal adalah persamaan bidang umum berbentuk A x + B y + C z + D = 0, yang memenuhi syarat berikut: panjang vektor n → = (A, B, C) sama dengan satu , yaitu. n → = A 2 + B 2 + C 2 = 1, dan D ≤ 0.
Selain itu, penulisan persamaan normal suatu bidang dapat berbentuk cos α · x + cos β · y + cos γ · z - p = 0, dimana P adalah bilangan non-negatif yang sama dengan jarak dari titik asal ke bidang, dan cos α, cos β, cos γ adalah cosinus arah dari vektor normal suatu bidang dengan satuan panjang tertentu.
n → = (cos α , cos β , cos γ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1
Artinya, menurut persamaan normal bidang, bidang pada sistem koordinat persegi panjang O x y z berjarak jauh dari titik asal. P dalam arah positif dari vektor normal bidang ini n → = (cos α, cos β, cos γ). Jika P sama dengan nol, maka bidang tersebut melewati titik asal.
Contoh 3
Bidang didefinisikan oleh persamaan bidang umum berbentuk - 1 4 · x - 3 4 · y + 6 4 · z - 7 = 0. D = - 7 ≤ 0, vektor normal bidang ini n → = - 1 4, - 3 4, 6 4 panjangnya sama dengan satu, karena n → = - 1 4 2 + - 3 4 2 + 6 4 = 1. Oleh karena itu, persamaan bidang umum ini merupakan persamaan bidang normal.
Untuk mempelajari lebih detail tentang persamaan bidang normal, kami sarankan untuk membuka bagian yang sesuai. Topiknya membahas analisis masalah dan contoh tipikal, serta metode untuk membawa persamaan umum bidang ke bentuk normal.
Bidang tersebut memotong ruas-ruas yang panjangnya tertentu pada sumbu koordinat O x, O y dan O z. Panjang segmen ditentukan oleh bilangan real bukan nol a, b, dan c. Persamaan bidang pada segmen berbentuk x a + y b + z c = 1. Tanda bilangan a, b dan c menunjukkan ke arah mana dari nilai nol ruas-ruas pada sumbu koordinat harus diplot.
Contoh 4
Mari kita buat sebuah bidang dalam sistem koordinat persegi panjang, yang ditentukan oleh persamaan rumus bidang pada ruas x - 5 + y - 4 + z 4 = 1.
Titik-titik tersebut dipindahkan dari titik asal pada arah negatif sebanyak 5 satuan sepanjang sumbu absis, sebanyak 4 satuan pada arah negatif sepanjang sumbu ordinat, dan sebanyak 4 satuan pada arah positif sepanjang sumbu aplikasi. Tandai titik-titik tersebut dan hubungkan dengan garis lurus.
Bidang segitiga yang dihasilkan adalah bidang yang sesuai dengan persamaan bidang dalam segmen-segmen, berbentuk x - 5 + y - 4 + z 4 = 1.
Informasi lebih rinci tentang persamaan bidang dalam segmen dan membawa persamaan bidang dalam segmen ke persamaan umum bidang tersedia pada artikel tersendiri. Ada juga sejumlah solusi untuk masalah dan contoh mengenai topik tersebut.
Jika Anda melihat kesalahan pada teks, silakan sorot dan tekan Ctrl+Enter