Fractal geometry of the world. Fractal geometry is the genetic code of the Universe

Content

Introduction

The concept of a fractal................................................... .........................................4

The history of the appearance of fractals………………………………………………………........6

Algebraic fractals………………..…………………………….8

Maldebrod set……………………………………………...9
Julia set……………………………………………………11
Newton's pools (fractals)……………………………………………………13
Fractal (bubbles) Halley……………………………………………..14

Practical use fractals…………………………………...15

Conclusion……………………………………………………………………………….19

List of references……………………………………………………………...…20

Introduction

The language of science is rapidly changing in the modern world. The history of the development of physics goes back more than one century. During this time, a huge number of diverse natural phenomena have been studied, fundamental laws of physics have been discovered that explain various experimental facts.

Most systems in nature combine two properties: firstly, they are very large, often multifaceted, diverse and complex, and Secondly they are formed under the influence of a very small number of simple laws, and then develop, obeying these simple laws. These are the most different systems, starting from crystals and simply clusters (various types of clusters, such as clouds, rivers, mountains, continents, stars), ending with ecosystems and biological objects (from a fern leaf to the human brain). Fractals are just such objects: on the one hand, complex (containing infinitely many elements), on the other hand, built according to very simple laws. Thanks to this property, fractals have much in common with many natural objects. But a fractal compares favorably with a natural object in that a fractal has a strict mathematical definition and is amenable to strict description and analysis. Therefore, the theory of fractals makes it possible to predict the growth rate of plant root systems, labor costs for draining swamps, the dependence of straw mass on shoot height, and much more. This is a new direction in mathematics, which has made a revolution in the scientific paradigm, comparable in significance to the theory of relativity and quantum mechanics. Objects of fractal geometry in their own way appearance sharply different from the “regular” geometric shapes we are used to. In fact, this is a breakthrough in the mathematical description of systems that for a long time did not lend themselves to such description.

Fractal geometry is not a “pure” geometric theory. It is rather a concept, a new look at well-known things, a restructuring of perception that forces the researcher to see the world in a new way.

The purpose of my work is to familiarize ourselves with the concept of “fractal” and its variety “algebraic fractal”.

Fractal concept

Relatively recently, in mathematics, an image of an object arose, more voluminous, but nevertheless similar to a line. Some scientists found it difficult to come to terms with the concept of a line having no width, so they gradually began to study geometric shapes and structures having fractional spatial dimension. Continuous curves, which have all their derivatives, were replaced by broken or very jagged curves. A striking example of such a curve is the trajectory of a Brownian particle. This is how the concept of a fractal arose in science.

Fractal(Latin fractus - crushed, broken, broken) - a complex geometric figure that has the property of self-similarity, that is, composed of several parts, each of which is similar to the entire figure (Fig. 1). In a broader sense, fractals are understood as sets of points in Euclidean space that have a fractional metric dimension (in the sense of Minkowski or Hausdorff) or a metric dimension.

Rice. 1
It should be noted that the word “fractal” is not a mathematical term and does not have a generally accepted strict mathematical definition. It can be used when the figure in question has any of the following properties:

It has a non-trivial structure on all scales. This is in contrast to regular figures (such as a circle, ellipse, graph smooth function): If we look at a small fragment of a regular figure on a very large scale, it will look like a fragment of a straight line. For a fractal, increasing the scale does not lead to a simplification of the structure; on all scales we will see an equally complex picture.

Is self-similar or approximately self-similar.

It has a fractional metric dimension.

Many objects in nature have fractal properties, for example, coasts, clouds, tree crowns, the circulatory system and the alveolar system of humans or animals.
Fractals, especially on a plane, are popular due to the combination of beauty with the ease of construction using a computer.

The history of fractals

The study of fractals at the turn of the 19th and 20th centuries was more episodic than systematic, because previously mathematicians mainly studied “good” objects that could be studied using common methods and theories. In 1872, the German mathematician Karl Weierstrass constructed an example of a continuous function that is nowhere differentiable, that is, does not have a tangent at any of its points. However, its construction was entirely abstract and difficult to understand. Therefore, in 1904, the Swede Helge von Koch came up with a continuous curve that has no tangent anywhere, and is quite easy to draw. It turned out that it has the properties of a fractal. One variant of this curve is called the “Koch snowflake”.
The ideas of self-similarity of figures were picked up by the Frenchman Paul Pierre Levy, the future mentor of Benoit Mandelbrot. In 1938, his article “Plane and spatial curves and surfaces consisting of parts similar to the whole” was published, which described another fractal - the Levy C-curve. All of these fractals listed above can be conditionally classified as one class of constructive (geometric) fractals.
Another class is dynamic (algebraic) fractals, which include the Mandelbrot set. The first research in this direction began at the beginning of the 20th century and is associated with the names of the French mathematicians Gaston Julia and Pierre Fatou. In 1918, Julia's work was published on iterations of complex rational functions, which describes Julia sets, a whole family of fractals closely related to the Mandelbrot set. This work was awarded a prize by the French Academy, but it did not contain a single illustration, so it was impossible to appreciate the beauty of the open objects

The first ideas of fractal geometry arose in the 19th century. Cantor, using a simple recursive (repeating) procedure, turned the line into a collection of unconnected points (the so-called Cantor Dust). He would take a line and remove the central third and then repeat the same with the remaining sections. (Fig. 2)

Rice. 2

Peano drew a special kind of line.(Fig. 3)

Rice. 3

To draw it, Peano used the following algorithm.

In the first step, he took a straight line and replaced it with 9 segments 3 times shorter than the length of the original line (part 1 and 2 of the picture). Then he did the same with each segment of the resulting line. And so on ad infinitum. The uniqueness of the line is that it fills the entire plane. It is proved that for every point on the plane one can find a point belonging to the Peano line.

Peano's curve and Cantor's dust went beyond ordinary geometric objects. They did not have a clear dimension. Cantor's dust seemed to be built on the basis of a one-dimensional straight line, but consisted of points (dimension 0). And the Peano curve was built on the basis of a one-dimensional line, and the result was a plane. In many other areas of science, problems appeared whose solution led to strange results similar to those described above (Brownian motion, stock prices).

Until the 20th century, data on such strange objects was accumulated, without any attempt to systematize them. That was until Benoit Mandelbrot, the father of modern fractal geometry and the word fractal, took up them. Gradually comparing the facts, he came to the discovery of a new direction in mathematics - fractal geometry.

To imagine a fractal more clearly, let’s consider an example given in B. Mandelbrot’s book “The Fractal Geometry of Nature”, which has become a classic - “What is the length of the coast of Britain?” The answer to this question is not as simple as it seems. It all depends on the length of the tool being used. By measuring the shore using a kilometer ruler, they get some length. However, many small bays and peninsulas are missed, which are much smaller in size than the measured ruler. By reducing the size of the ruler to 1 meter, it turns out that the length of the coast will become longer. When measuring the length of the bank using a millimeter ruler, taking into account parts that are larger than a millimeter, the length will be even greater. As a result, the answer to such a seemingly simple question can baffle anyone - the length of the coast of Britain is endless.

Algebraic fractals

Algebraic fractals got their name because they are built on the basis of algebraic formulas. There are several methods for obtaining algebraic fractals. One of the methods is to repeatedly calculate the function, wherez - complex number, and f is a certain function. The calculation of this function continues until a certain condition is met. And when this condition is met, a dot is displayed on the screen. In this case, the function values for different points of the complex plane can have different behavior:

tends to infinity over time;

tends to 0;
takes several fixed values and does not go beyond them;
behavior is chaotic, without any trends.

3.1 Mandelbrot set

The Mandelbrot set (one of the most famous fractal objects) was first constructed (visually using a computer) by Benoit Mandelbrot in the spring of 1980 at the IBM research center. Thomas J. Watson. And although research into such objects began in the last century, it was the discovery of this set and the improvement of computer graphics hardware that decisively influenced the development of fractal geometry and chaos theory. So, what is the Mandelbrot set?

Consider the function of a complex variable. Let's putand consider the sequence, where for any. Such a sequence can be bounded (i.e. there can be an r such that for any) or “run away to infinity” (i.e. for any r > 0 there is). The Mandelbrot set can be defined as the set of complex numbers c for which the specified sequence is bounded. Unfortunately, there is no known analytical expression that would allow a given c to determine whether it belongs to the Mandelbrot set or not. Therefore, to construct a set, a computer experiment is used: they look through a set of points on the complex plane with a certain step, and for each point they carry out a certain number iterations (find a certain number of members of the sequence) and watch its “behavior”. (Fig. 4).

It has been proven that the Mandelbrot set is located in a circle of radius r=2 with its center at the origin. Thus, if at some step the modulus of the next term of the sequence exceeds 2, we can immediately conclude that the point corresponding to c, which defines this sequence, does not belong to the Mandelbrot set.

By decreasing the step at which complex numbers are scanned and increasing the number of iterations, we can obtain as detailed as we like, but always only approximate images of the set.

Let us have N colors at our disposal, numbered for definiteness from 0 to N-1. We will assume, again for definiteness, that black color has number 0. If for a given c after N-1 iterations the point does not go beyond the circle of radius 2, we will assume that c belongs to the Mandelbrot set and paint this point c black. Otherwise, if at some step k (k Є ) the next point went outside the circle of radius 2 (i.e. at the kth step we realized that it was “running away”), paint it in color k.

Beautiful images are obtained with a successful choice of palette and neighborhood of the set (namely, outside the set we will get “colored dots”) (Fig. 5, 6).

Rice. 4

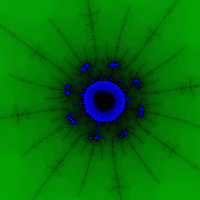
Rice. 5 Fig. 6

3.2 Julia set

Julia sets, closely related to the Mandelbrot set, were studied at the beginning of the 20th century by mathematicians Gaston Julia and Pierre Fatou (see). In 1917-1919 they obtained fundamental results related to iteration of functions of a complex variable. Generally speaking, this fact deserves a separate discussion and is an impressive example of mathematical research, many decades ahead of its time (scientists could only approximately imagine what the objects they studied looked like!), but we will only describe a method for constructing Julia sets for a function of a complex variable. More precisely, we will build the so-called. "filling Julia sets".

Consider a rectangle (x 1 ;y 1 )-(x 2 ;y 2 ). Let's fix the constant c and begin to view the points of the selected rectangle with a certain step. For each point, as in constructing the Mandelbrot set, we will carry out a series of iterations (the greater the number of iterations, the more accurate the set will be obtained). If after a series of iterations the point does not “run away” beyond the border of the circle of radius 2, we will paint it with black color, otherwise with a color from the palette. (Fig. 7, 8, 9, 10).

Rice. 7

Fig.8 Fig. 9

Rice. 10

3.3 Newton's pools (fractals)

Another type of dynamic fractals are Newtonian fractals (so-called basins). (Fig. 11). The formulas for their construction are based on the method of solving nonlinear equations, which was invented by the great mathematician back in the 17th century. Applying general formula Newton's method zn+1 = zn - f (zn)/f"(zn), n=0, 1, 2… to solve the equation f (x)=0 to the polynomial zk-a, we obtain a sequence of points: zn+1 = (k-1)znk/kznk-1, n=0, 1, 2... Choosing various complex numbers z0 as initial approximations, we will obtain sequences that converge to the roots of this polynomial. Since it has exactly k roots, then the entire plane is divided into k parts - areas of attraction of roots.The boundaries of these parts have a fractal structure.

Rice. eleven

3.4 Fractal (bubbles) Halley

Such fractals are obtained if, as a rule for constructing a dynamic fractal, one uses Halley’s formula to find approximate values of the roots of a function. (Fig. 12).

The method consists of a sequence of iterations:

The idea of the method is almost the same as that used for drawing dynamic fractals: we take some initial value (as usual, here we are talking about values of variables and functions) and apply the formula to it many times, obtaining a sequence of numbers. It almost always converges to one of the zeros of the function (that is, the value of the variable at which the function takes the value 0). Halley's method, despite the cumbersome formula, works more effective than the method : The sequence converges to zero functions faster.

Rice. 12

Practical application of fractals

Fractals are increasingly used in science. The main reason for this is that they describe real world sometimes even better than traditional physics or mathematics. Here are some examples.

Computer systems

Of all the images a computer can create, few can rival fractal images when it comes to true beauty.

Most useful use Fractals in computer science are fractal data compression. This type of compression is based on the fact that the real world is well described by fractal geometry. At the same time, images are compressed much better than is done with conventional methods (such as jpeg or gif). Another advantage of fractal compression is that when the image is enlarged, there is no pixelation effect (increasing the size of the dots to sizes that distort the image). With fractal compression, after enlargement, the picture often looks even better than before.

Fluid mechanics

The study of turbulence in flows is very well adapted to

fractals. Turbulent flows are chaotic and therefore difficult to model accurately. And here the transition to a fractal representation helps, which greatly facilitates the work of engineers and physicists, allowing them to better understand the dynamics of complex flows.

Using fractals you can also simulate flames.

Porous materials are well represented in fractal form due to the fact that they have a very complex geometry. It is used in petroleum science.

Telecommunications

To transmit data over a distance, antennas with

fractal shapes, which greatly reduces their size and weight. Fractals are used to describe the curvature of surfaces. An uneven surface is characterized by a combination of two different fractals.
Medicine

Biosensory interactions. Heartbeat.
Biology

Modeling of chaotic processes, in particular when describing population models.
Nanotechnology

In the case of nanotechnology, fractals also play a role important role, since, due to their hierarchical self-organization, many nanosystems have a non-integer dimension, that is, they are fractals in their geometric, physicochemical or functional nature. For example, a striking example of chemical fractal systems are molecules "dendrimers » . (Fig. 13)

Rice. 13

Literature

Among literary works find those that have a textual, structural or semantic fractal nature. In text fractals, elements of the text are potentially endlessly repeated (“The priest had a dog...”, “The parable of the philosopher who dreams that he is a butterfly who dreams that she is a philosopher who dreams...” and texts with extensions (“The house that he built Jack")

In structural fractals, the text scheme is potentially fractal: wreath of sonnets (15 poems), wreath of wreaths of sonnets (211 poems), wreath of wreaths of sonnets (2455 poems).

Conclusion

A fractal is an object of infinite complexity, allowing you to see as many of its details up close as from afar. The Earth is a classic example of a fractal object. From space it looks like a ball. If we approach it, we will find oceans, continents, coastlines and mountain ranges. Let's look at the mountains closer - even finer details will become visible: a piece of land on the surface of the mountain, in its scale, is as complex and uneven as the mountain itself. And even greater magnification will reveal tiny particles of soil, each of which is itself a fractal object.

In conclusion, I would like to say that after fractals were discovered, it became obvious to many scientists that the good old forms of Euclidean geometry are much inferior to most natural objects due to the lack of some irregularity, disorder and unpredictability in them. It is possible that new ideas of fractal geometry will help to study many mysterious phenomena surrounding nature. Currently, fractals are rapidly invading many areas of physics, biology, medicine, sociology, and economics. Image processing and pattern recognition methods that use new concepts enable researchers to use this mathematical apparatus to quantitatively describe a huge number of natural objects and structures.

Bibliography

1. Introduction to fractals,

2. Zhikov V.V. On Julia sets. // Modern natural science: Encyclopedia: In 10 volumes. T.1: Mathematics. Mechanics. M., 2000.

3. Zhikov V.V. Fractals. // Modern natural science: Encyclopedia: In 10 volumes. T.1: Mathematics. Mechanics. M., 2000.

4. Mandelbrot B. Fractal geometry of nature. – M: Institute of Computer Research, 2002.

5. Morozov A.D. Introduction to the theory of fractals. -Moscow-Izhevsk: Institute of Computer Research, 2002, 160pp.

6. Dynamic (algebraic) fractals // Elements.. URL:http:// elementy. ru/ posters/ fractals/ dynamic

7. Dynamic (algebraic) fractals // Elements.. URL:http:// elementy.ru/posters/fractals/Mandelbrot#nop

8. Algebraic fractals // Fractals.. URL:http://rusproject.narod.ru/article/fractals.htm

In Chapters 6 and 7, we introduced the Koch and Peano curves using geomorphology to help us, but the most significant applications of fractal theory are in somewhat different areas. Slowly approaching the main trends in science, we will consider in this chapter (and in the next two) two questions of exceptional antiquity, importance and complexity.

The distribution of stars, galaxies, clusters of galaxies and similar matters have long fascinated both amateurs and specialists, but clustering still remains on the periphery of astronomy, and astrophysics in general. main reason is that no one has been able to explain why the distribution of matter obeys irregular hierarchical laws - at least within a certain range of scales. In many works devoted to this topic, one can find mention of the phenomenon of clustering, but in serious theoretical studies, it is usually hastily swept under the rug, claiming that galaxies are distributed quite uniformly - on a scale exceeding some large but undefined threshold.

Looking at the situation from a less fundamental perspective, we can say that the reluctance to deal with the irregular stems from the lack of tools for its mathematical description. The statistician is required to choose between two assumptions, of which only one can be considered thoroughly examined (asymptotic homogeneity). Is it any wonder that the results are, to put it mildly, inconclusive?

The questions, however, are such that they are difficult to dismiss. I think it is absolutely necessary - in parallel with continuing to try to explain clustering - to find a way to describe it and model reality purely geometric means. By approaching this topic from a fractal perspective over several chapters of this essay, we hope to show through explicit models that the evidence suggests a degree of clustering that goes far beyond the limits set for it by existing models.

This chapter should be considered introductory: here we will get acquainted with one very influential theory of the formation of stars and galaxies proposed by Hoyle, with the basic formal model of their distribution, which we owe to Fournier d'Albu (this model is also known as the Charlier model), and, most importantly, important, we will obtain some empirical data. We will show that both the theory and the data can be interpreted in terms of the concept of scale-invariant fractal dust. I insist that the distribution of galaxies and stars includes a certain zone of self-similarity, within which the fractal dimension satisfies inequality In addition, the theoretical reasons why one might expect , and, as a consequence, discusses why the observed value is .

Announcement. In Chapter 22, we will use fractal tools to improve our understanding of the meaning of the cosmological principle, consider how it can and should be modified, and learn why such modification necessarily requires randomness. We will defer discussion of clusters within the improved model until Chapters 22, 23, and 32 to 35.

IS IT POSSIBLE TO TALK ABOUT GLOBALdensityMATTER?

Let's start by taking a closer look at the concept of global matter density. As in the case of coastlines, everything here, at first glance, looks very simple, but in reality it very quickly - and very interestingly - gets confused. To determine and measure density, one starts with a mass concentrated inside a sphere of radius with a center coinciding with the center of the Earth. This estimates the approximate density, defined as

After this, the value tends to infinity, and the global density is defined as the limit to which the approximate density converges in this case.

However, does global density necessarily converge to a positive and finite limit? If so, then the speed of such convergence leaves much to be desired, and that’s putting it mildly. Moreover, estimates of the maximum density, when considered in a time perspective, behave rather strangely. As the telescopic depth of the universe increased, the approximate density decreased in a surprisingly systematic manner. According to de Vaucouleurs, there has always been a decrease. The observed index is less than 3 - in the best approximation.

De Vaucouleurs put forward the thesis that the behavior of the approximate density value reflects reality, meaning that . This formula brings to mind the classic result for a ball of radius embedded in a Euclidean space of dimension - the volume of such a ball. In Chapter 6, we encountered the same formula for the Koch curve, with the only difference that the indicator there was not the Euclidean dimension, but a fractional fractal dimension. And in Chapter 8 we received the formula for Cantor's drink on the time axis (here).

All these precedents force (and very persistently) to assume that the de Vaucouleurs exponent is nothing more than a fractal dimension.

ARE STARS IN THE RANGE OF SCALE INVARIANCE?

Obviously, the range of scale invariance in which the inequality is satisfied should not include objects with explicitly defined boundaries - such as planets. But are the stars included in it? According to the data obtained by Webbick and presented in, the mass of the Milky Way inside the radus sphere can be quite represented in the form , where the value is extrapolated from the galaxies. We will, however, continue our discussion solely in galactic terms.

DOES THE RANGE OF SCALE INVARIANCE HAVE AN UPPER THRESHOLD?

The question of how far towards very large scales the range within which extends is very controversial, and in Lately he drew attention to himself again. Many authors either explicitly state or imply that this range allows for the existence of an outer limit corresponding to the size of galaxy clusters. Other authors express their disagreement with this opinion. De Vaucouleurs argues that “clustering of galaxies, and perhaps all other forms of matter, is a dominant feature of the structure of the Universe at all observable scales, with no indication of any approximation to homogeneity; average density matter decreases steadily as larger volumes of space are taken into account, and we have no experimentally verified reason to believe that this trend does not extend over much greater distances and lower densities.”

The debate between these two schools is certainly very interesting and important - for cosmology, but not for our essay. Even if the range in which , has boundaries on both sides, its very existence is significant enough to justify the most careful study.

In any case, the Universe (just like that ball of thread we talked about in Chapter 6) appears to have a number of different effective dimensions. If we start with scales on the order of the radius of the Earth, then the first dimension we encounter will be 3 (this is the dimension solids with a clear boundary). Further, the dimension drops to 0 (since matter is considered as a cluster of isolated points). Next comes a very interesting section, characterized by a certain non-trivial dimension that satisfies the inequality . If scale-invariant clustering continues to infinity, then the series of effective dimensions ends at this last value. If there is a finite external threshold, then a fourth interval of dimensions is added to the list, within which the points lose their individuality, and we have a homogeneous gas on our hands, i.e., the dimension returns to 3 again.

The most naive idea is that galaxies are distributed approximately uniformly in the Universe. In this case, the sequence of dimensions D is reduced to three values: 3, 0 and again 3.

< Общая теория относительности утверждает, что при отсутствии материи локальная геометрия пространства стремится стать плоской и евклидовой, в то время как присутствие материи переводит ее в локально риманову. Здесь мы можем говорить о глобально плоской Вселенной, размерность которой равна 3 с локальными значениями . Такой тип возмущений описан в , довольно туманной работе, автор которой приводит (с. 312) пример построения кривой Коха (см. главу 6), не ссылаясь при этом на самого Коха.

FOURNIER'S UNIVERSE

All we have to do is construct a fractal that satisfies the rule and see how it agrees with generally accepted views of the Universe. The first detailed model of this kind was proposed by E. E. Fournier d'Albom (see Chapter 40). Although Fournier's book is largely fiction disguised as scientific research, it does contain several extremely interesting considerations that we will discuss shortly.First, it seems to me, we should describe the structure proposed by Fournier.

We begin the construction with a regular octahedron, the projection of which is shown in the center of Fig. 141. The projection shows the four corners of a square, the diagonal of which is 12 "units", and the center of this square. However, the octahedron has two more points above and below our plane on a perpendicular drawn through the center of the square, at the same distance of 6 “units” from this center.

Next, each point is replaced by a ball of radius 1, which we will consider as a “zero-order stellar aggregate.” The smallest ball containing all 7 original balls will be called a “stellar aggregate of the first order”. A second-order aggregate is obtained by increasing the first-order aggregate by a factor and replacing each of the new balls of radius 7 with a copy of the first-order aggregate. Similarly, a third-order aggregate is obtained by increasing the second-order aggregate by a factor and replacing each of the balls with a copy of the second-order aggregate. And so on.

In short, when transitioning between neighboring orders of aggregation, both the number of points and the radius of the balls increases by a factor. Consequently, for any value that is the radius of any aggregate, the function that determines the number of points contained in a ball of radius has the form . For intermediate ones, the function takes smaller values (reaching ), however, according to the general tendency, .

It is also possible to interpolate zero-order aggregates in successive steps to aggregates of order -1, -2, etc. At the first stage, we replace each zero-order aggregate with a copy of the first-order aggregate, reduced by a ratio of 1/7, and so on. With this construction, the relation remains true for increasingly smaller values. After endless extra- and interpolation, we obtain a self-similar set of dimension .

In addition, the dimension of an object in 3-space does not necessarily oblige it to be a straight line or any other rectifiable curve. He doesn't even have to be coherent. Each dimension is compatible with any smaller or equal topological dimension. In particular, the topological dimension of the Fournier universe, infinite in both directions, is equal to 0, since it is completely disconnected “dust”.

MASS DISTRIBUTION: FRACTAL HOMOGENEITY

The step from geometry to mass distribution seems to me as clear as possible. If each stellar aggregate of zero order is loaded with unit mass, then the mass inside the ball of radius is identical to the value , and therefore . Moreover, in order to obtain aggregates of order -1 from aggregates of order zero, it is necessary to break up a ball that we considered homogeneous and discover that it consists of seven smaller balls. At this stage, the rule also applies to radii smaller than unity.

Considering the resulting distribution of mass over the entire 3-space, we see that it is extremely inhomogeneous, although on the Fournier fractal it has no equal in homogeneity. (Recall Fig. 120.) In particular, any two geometrically identical parts of the Fournier universe contain the same masses. I propose to call this mass distribution fractally homogeneous.

< Предыдущее определение сформулировано в терминах масштабно-инвариантных фракталов, но концепция фрактальной гомогенности в общем случае гораздо шире. Она применима к любому фракталу, для которого положительна и конечна хаусдорфова мера в размерности . Фрактальная гомогенность требует, чтобы масса, содержащаяся в множестве, была пропорциональна хаусдорфовой мере этого множества.

FOURNIER'S UNIVERSE IS LIKE CANTOR'S DUST. EXPANSION D0

I hope that the reader is not confused by the careless use of fractal terminology in the early sections of this chapter. It is obvious that Fournier, without realizing it, was following a path parallel to that of his contemporary Cantor. The main difference is that Fournier's construction is embedded in space rather than in an interval on a line. To further enhance the similarity, it is enough to replace the spherical Fournier aggregates with blocks (filled cubes). Each zero-order aggregate becomes a block whose side length is 1, and includes 7 smaller aggregates with a side of 1/7: the center of one of them coincides with the center of the original cube, and the other six touch the central sub-squares on the faces of the original cube.

Below we will look at how Fournier derived meaning from the fundamental physical phenomenon, and how Hoyle arrived at the same result. From a geometric point of view, the case is special, even if throughout the entire construction we adhere to the octahedron shape and value. Since the balls do not overlap each other, the value can take any value in the range from 3 to infinity, resulting in the law where over the entire interval from 0 to .

THE CHARLIER MODEL AND OTHER FRACTAL UNIVERSE

The above constructions did not avoid any of the shortcomings characteristic of the first fractal models. What is most striking is that Fournier's model, like the Koch curve model in Chapter 6 and the Cantor dust model in Chapter 8, is grotesquely correct. To correct the situation, Charlier proposed providing the ability to move from one hierarchical level to another, taking values and .

Charlier's reputation in scientific circles was so high that, despite all his generous praise of Fournier, expressed in all the leading languages of science of the time, even the original model soon began to be attributed to the famous interpreter, and not to anyone. famous author. The new model was widely discussed at the time, especially in . Moreover, it attracted the attention of the highly influential Emile Borel, whose comments are very insightful, if somewhat dry. However, since then, apart from several frantic attempts to bring it to light, Charlier’s model has been in oblivion (not very convincing reasons for such oblivion are set out in, pp. 20-22 and 408-409). However, she stubbornly refuses to die. The main idea has already been discovered many times by different researchers independently of each other; I especially recommend taking a look at. (Also see PAUL LEVY's section in Chapter 40.) What I find most important, however, is that the fractal basis of Fournier's universe is implicit in the discussion of turbulence and galaxies in the work (see Chapter 10) and in the model of galactic genesis, proposed by Hoyle (we will consider it below).

The main fractal component is also present in my models (see chapters 32 to 35).

In this light, the question arises: could a galaxy distribution pattern not be a fractal with one or two thresholds? I think no. If we agree that the distribution must be scale-invariant (the reasons for this are outlined in Chapter 11), and that the set on which matter is concentrated is not a standard scale set, we have no choice but to accept fractality of this set.

Given the importance of scale invariance, it is not difficult to understand why Charlier's scale-free generalization of the Fournier model was doomed from the start.< Оно, кстати, позволяет величине vary depending on that within two boundaries, and . Here is another topic for discussion: the effective dimension does not have to have one single value, this value can float between the upper and lower limits. We will return to this topic in Chapter 15.

WHY DID FOURNIER EXPECTD= 1?

Let us now discuss the very impressive argumentation that led Fournier to the conclusion that the indicator should be equal to 1 (see, p. 103). This argument in itself is a serious argument in favor of not forgetting the name of its author.

Let us consider a galactic aggregate of arbitrary order with mass and radius . Discarding fruitless doubts and applying the formula for objects with spherical symmetry to this case, let us assume that the gravitational potential on the surface of the sphere is equal to ( - gravitational constant). A star falling on our Universe collides with its surface at a speed .

According to Fournier, a very important conclusion can be drawn from the fact that no observable star moves at a speed exceeding 1/300 of the speed of light. The mass contained inside the world ball increases in direct proportion to its radius, and not to its volume, or, in other words, the density of matter inside the world ball is inversely proportional to its surface area... Let us explain the last statement - the potential on the surface of the sphere is always the same, since it is directly proportional to the mass of matter inside the sphere and inversely proportional to the distance from the center. As a consequence, stellar velocities close to the speed of light are not common in any part of the Universe.

CUTTING ON HOYLE; JEANS CRITERION

Hierarchical distribution also appears in Hoyle's theory (see), according to which galaxies and stars are formed through a cascade process, and this process begins with a homogeneous gas.

Let us consider a gas cloud of mass , heated to a temperature and distributed with uniform density inside a ball of radius . As Gine showed, when a “critical” situation arises. (Here is Boltzmann's constant, a is a numerical coefficient.) Being in a critical state, the primary gas cloud is unstable and must inevitably shrink.

Hoyle postulates that (a) the magnitude reaches a critical value somewhere at the very beginning, (b) compression stops when the volume of the gas cloud is reduced to 1/25 of its original volume, and (c) each cloud at this stage breaks up into five smaller ones clouds with same sizes, masses and radii. That is, the process returns to the same place where it began: its result is an unstable state, followed by a second stage of compression and separation, then a third, etc. The collapsing stops only when the clouds become so opaque that they retain the resulting When gas is compressed, there is heat inside.

As in various other areas in which similar cascade processes occur, I propose to apply general terminology to this case, that is, we will call the five clouds curds, and the cascade process itself - curdling. As I mentioned when introducing the last term, I simply could not resist the allusions to galaxies.

For the sake of convenience in graphically representing his model, Fournier introduces , while Hoyle claims that the value is physically justified. The detailing of Fournier's geometric illustration goes beyond any reasonable or necessary limits. Hoyle's statements regarding the spatial structure of cottage cheese, on the contrary, are rather vague. We will have to wait until Chapter 23, where we look at random folding, for a detailed implementation of Hoyle's model. Be that as it may, the mentioned discrepancies are not of fundamental importance: the main thing is the fact that, i.e., the indicator must become an integral part of our construction if we want the curdling to end in the same state from which it began, - and namely, the instability of Jeans.

In addition, if the duration of the first stage is taken as 1, then, according to gas dynamics data, the duration of that stage will be . Consequently, the total duration of the entire process, consisting of an infinite number of stages, does not exceed 1.2500.

EQUIVALENCE OF FOURNIER AND HOYLE APPROACHES TO CONCLUSIOND= 1

At the boundary of an unstable gas cloud that satisfies the Jeans criterion, the velocity and temperature are related by the relation , since they are equal to both (Fournier) and (Gene). Let us now remember that in statistical thermodynamics the temperature of a gas is directly proportional to the root-mean-square velocity of its molecules. This means, from a combination of the Fournier and Jeans criteria, we can assume that at the cloud boundary the speed of fall of a macroscopic object is directly proportional average speed its molecules. A careful analysis of the role of temperature in the Jeans criterion will certainly show that these two criteria are equivalent.< Вероятнее всего, аналогия распространяется и на справедливость отношения внутри галактик, о чем сообщает Валленквист в .

WHYD= 1.23, AND NOTD= 1?

The discrepancy between the empirical meaning and the theoretical meaning of Fournier and Hoyle raises important problem. P. J. E. Peebles examined it in 1974 from the perspective of the theory of relativity. In his work, the physical and statistical (but not geometric) aspects of the mentioned problem received exhaustive coverage.

FRACTAL DIMENSION OF THE SKY

The sky is a projection of the Universe. To obtain this projection, each point of the Universe is first described by spherical coordinates , and , and then the coordinate is replaced by 1. If the Universe is a fractal with dimension , and the origin of the reference system belongs to this very Universe (see Chapter 22), then the structure of the projection, as a rule, , is defined by the following alternative: implies that the projection covers some non-zero area of the sky, while means that the projection itself has a fractal dimension.< Как показано на рис. 141 и 143, «правило» не лишено исключений, обусловленных структурой фрактала и/или/ выбором точки отсчета. О таких правилах часто говорят «истинно с вероятностью 1».

A NOTE ABOUT THE BURNING SKY EFFECT (INCORRECTLY CALLED OLBERS' PARADOX)

The rule from the previous section has a lot to do with the motivation that led various researchers (including Fournier) to discover their own versions of the fractal universe. They understood that such universes geometrically “cancel” the effect of the burning sky, which is also often (but incorrectly) called Olbers’ paradox. If we assume that the distribution of celestial bodies is uniform (that is, on all scales), then the sky above us should be almost uniformly illuminated both at night and during the day, and the brightness of this illumination should be comparable to the sun.

This paradox no longer interests physicists, having been nullified by the theory of relativity, the theory of the expanding Universe and other considerations. However, his death had an interesting side effect: numerous commentators began to quote their favorite explanations for the blazing sky effect - some in the hope of justifying their disdain for clustering, while others, on the contrary, completely denying its reality. A very strange point of view, I must say. Even if we assume that galaxy clustering has nothing to do with the absence of the burning sky effect, it still exists - and requires proper study. Moreover, as we will see in Chapter 32, the concept of an expanding universe is compatible not only with standard homogeneity, but also with fractal homogeneity.

The effect of a blazing sky is explained very simply. Since the amount of light emitted by a star is directly proportional to its surface area, the amount of light reaching an observer located at a distance from the star must be , but the visible surface area of the star must also be . Thus, the ratio of the amount of light to the apparent spherical angle does not depend on . In addition, if the distribution of stars in the Universe is uniform, then almost any direction you look in will sooner or later encounter some star. Consequently, the sky is evenly illuminated by starlight and appears glowing. (The lunar disk in this case forms an exclusively dark region - at least in the absence of atmospheric diffusion.)

If we assume that the Universe is fractal and that its dimension is , then the paradox resolves itself. In this case, the projection of the Universe onto the firmament is a fractal set of the same dimension, i.e. a set of zero area. Even if the stars have a non-zero radius, most of the directions go to infinity without meeting a single star on their way. If we look along these directions, we will see only the blackness of the night sky. If an interval in which , is followed by an interval in which , then the background of the sky will not be strictly black, but extremely dimly lit.

Kepler drew attention to the effect of the burning sky shortly after Galileo, in his “Star Message,” spoke favorably of the idea of a limitless Universe. In his “Conversation with the Starry Messenger” (1610), Kepler raised the following objection: “You do not hesitate at all to declare that more than 10,000 stars are visible to view... If this is so, and if [the stars] are of the same nature as our Sun, then why don’t all these suns collectively exceed our Sun in brightness?... Maybe they are eclipsed by the ether? Not in the slightest degree... It is absolutely obvious that our world cannot in any way belong to a disorderly swarm of countless other worlds” (see, pp. 34-35).

The conclusion was quite controversial, but the argumentation was not forgotten - evidence of this is the remark of Edmund Halley (made by him in 1720): “I have heard of another objection, which says that if the number of fixed stars were more than finite, then the entire arch of their visible sphere would be completely illuminated.” This objection was later discussed by de Chezo and I. G. Lambert, but its authorship was attributed to great friend Gauss to the German astronomer Olbers. The term "Olbers' paradox", which has since been used to describe this contradiction, is scandalous but symptomatic. The results of observations that fall into the category of “not subject to classification” (see p. 51) are often attributed to the first representative of the Official Majority, who will decorate them with a completely classifiable wrapper, even if only temporary. A discussion of the subject in historical perspective can be found in.

A NOTE ON NEWTONIAN GRAVITY

Reverend Bentley kept pestering Newton with one observation closely related to the burning sky effect: if the distribution of stars is uniform, then the force with which they act on each other is infinite. We can add that their gravitational potential is also infinite. And that any distribution in which , will give at large an infinite potential in all cases except . Modern potential theory (Frostman's theory) confirms the fact that there is some special connection between Newtonian gravity and value. The indicator obtained by Fournier and Hoyle should also be attributed to the manifestations of this connection.< Положение Фурнье о том, что «гравитационный потенциал на поверхности сферы всегда одинаков», является центральным в modern theory potential. " The square of the velocity ratio postulated by Fournier is exactly in the middle of the mentioned interval.

AN AGGLUTINATED FRACTAL UNIVERSE?

Many researchers believe that the formation of stars and other celestial objects can be explained by an upward cascade (i.e., the gradual agglutination of highly dispersed dust particles into ever larger chunks), without wanting to hear anything about the descending cascade a 1a Hoyle (i.e., the gradual fragmentation of very large and dispersed masses into ever smaller parts).

A similar alternative arises in connection with the cascades postulated in the theory of turbulence (see Chapter 10). The Richardson cascade proceeds downward to increasingly smaller eddies, but upward cascades can also participate in the process (see Chapter 40, section LEWIS FRY RICHARDSON). Thus, it is hoped that the relationship between the downward and upward cascades will soon be properly explained.

FRACTAL ARRAYS OF TELESCOPE

There could hardly be a more appropriate final touch to this discussion than a remark regarding the instruments with which galaxies are observed. To improve the quality of observation, Dyson proposes replacing large single telescopes with arrays of small telescopes. The diameter of each of the small telescopes should be about 0.1 m (the size of the smallest optically significant atmospheric disturbance), their centers should form a fractal hierarchical pattern, and the connection between the telescopes will be provided by Curry interferometers. A rough analysis leads to the conclusion that as suitable value dimensions should be taken 2/3. Here is Dyson’s own conclusion: “A three-kilometer array of 1024 ten-centimeter telescopes interconnected by 1023 interferometers is not the most practical proposal today. [I put it forward] as a theoretical idea to show what could, in principle, be done here.”

REVIEW OF RANDOM FRACTAL MODELS OF GALAXY CLUSTERS

If we believe that it is possible to effectively describe the distribution of galaxies using randomly discovered fractal models that are neither complex nor universal, it should not be surprising that intentionally fractal random models can provide us with much more effective descriptions. To begin with, we can understand Hoyle folding much better by considering it in its proper environment, that is, among random fractals (see Chapter 23). Of even greater significance, in my opinion, are the random models I developed, which we will discuss in Chapters 32 through 35. One of the arguments in favor of considering multiple models is that improving the quality of the description comes at the cost of increased complexity. The second argument is that each model is built on a special fractal dust, each of which deserves separate consideration. Let us briefly consider these models in logical order.

Around 1965, I set out to provide the relation with a corresponding model in which the “center of the Universe” would be absent as a concept. I first achieved this goal using the random walk model described in Chapter 32. Then, as an alternative, I developed the trem model, the essence of which was that a certain set of mutually independent and randomly placed trems of a random radius were cut out of space, and the upper bound of the radius could reach an upper threshold, which could be finite or infinite.

Since both models were chosen purely for reasons of formal simplicity, I was pleasantly surprised by their predictive value. My theoretical correlation functions turned out to be in good agreement with the curve-fitted functions given by Peebles (see, pp. 243-249).< Точнее, два моих приближения совпали на двухточечной корреляции, случайные блуждания дали хорошую трех- и плохую четырехточечную корреляции, а сферические тремы оказались на высоте во всех известных корреляциях.

Unfortunately, the examples generated by these models look completely unrealistic. Using a concept I developed specifically for this purpose, which I will discuss in Chapter 35, my early models exhibit unacceptable lacunar properties. In the case of the trem model, this shortcoming can be corrected by introducing more complex trem forms. For the random walk model, I used a less lacunar “subordinator”.

Thus, the study of galaxy clusters has significantly stimulated the development of fractal geometry. At present, the range of applications of fractal geometry in the study of galaxy clusters has expanded significantly, going far beyond those general cleaning and debugging that we have undertaken in this chapter.

CUT DIAMONDS LIKE STARS

The distribution of diamond deposits in the earth's crust is very similar to the distribution of stars and galaxies in the firmament. Imagine a large map of the world, on which every diamond mine, every rich deposit - now being developed or already abandoned - is marked with a pin. If we look at the map from a sufficiently large distance, we will see that the distribution of pins is extremely uneven. There are a few isolated pins scattered here and there, but most are concentrated in a few blessed (or cursed) areas. The surface of the earth within these areas, in turn, is not at all evenly paved with diamonds. Taking a closer look at each of them, we again see that most of the area remains empty, while a few scattered sub-areas show a significantly increased concentration of diamonds. This process can be continued over several orders of magnitude.

Are you tempted to apply the concept of curdling in this context? For my part, I will say that such a model exists, it was proposed by de Wis, and we will consider it in Chapter 39 in the section NON-LACUNARY FRACTALS.

Fournier's book offers the following explanation for this illustration: “The multiverse, built on the principle of a cross or an octahedron, is not a plan of our world, but helps to show the possibility of the existence of an infinite number of similar successive universes without causing the effect of the “burning sky.” The amount of matter in each world sphere is directly proportional to its radius. This condition is necessary to comply with the laws of gravity and radiation. In some directions the sky appears completely black - despite the fact that the number of universes is infinite. "World number" in in this case is , not like in the real world." instead of . The construction is continued one step further than is possible in Fig. 141.

(Dynamic) fractals

Fractals of this type arise when studying nonlinear dynamic systems (hence the name). The behavior of such a system can be described by a complex nonlinear function (polynomial) f(z). Let's take some initial point z0 on the complex plane. Now consider an infinite sequence of numbers on the complex plane, each of which is obtained from the previous one: z0, z1 = f(z0), z2 = f(z1), ... zn+1 = f(zn). Depending on the initial point z0, such a sequence can behave differently: tend to infinity as n → ∞; converge to some end point; cyclically take a series of fixed values; More complex options are also possible.

Thus, any point z of the complex plane has its own behavior during iterations of the function f(z), and the entire plane is divided into parts. Moreover, the points lying on the boundaries of these parts have the following property: with an arbitrarily small displacement, the nature of their behavior changes sharply (such points are called bifurcation points). So, it turns out that sets of points that have one specific type of behavior, as well as sets of bifurcation points, often have fractal properties. These are the Julia sets for the function f(z).

The Mandelbrot set is constructed somewhat differently. Consider the function fc(z) = z2 + c, where c is a complex number. Let us construct a sequence of this function with z0 = 0; depending on the parameter c, it can diverge to infinity or remain limited. Moreover, all values of c for which this sequence is limited form the Mandelbrot set. It was studied in detail by Mandelbrot himself and other mathematicians, who discovered many interesting properties of this set.

It can be seen that the definitions of the Julia and Mandelbrot sets are similar to each other. In fact, these two sets are closely related. Namely, the Mandelbrot set is all values of the complex parameter c for which the Julia set fc(z) is connected (a set is called connected if it cannot be divided into two disjoint parts, with some additional conditions).

This is the largest group of fractals. They are obtained using nonlinear processes in n-dimensional spaces. Two-dimensional processes are the most studied. When interpreting a nonlinear iterative process as a discrete dynamic system, one can use the terminology of the theory of these systems: phase portrait, steady-state process, attractor, etc.

It is known that nonlinear dynamic systems have several stable states. The state in which the dynamic system finds itself after a certain number of iterations depends on its initial state. Therefore, each stable state (or, as they say, attractor) has a certain region of initial states, from which the system will necessarily fall into the final states under consideration. Thus, the phase space of the system is divided into areas of attraction of attractors. If the phase space is two-dimensional, then coloring the areas of attraction different colors, you can obtain a color phase portrait of this system (iterative process). By changing the color selection algorithm, you can get complex fractal patterns with bizarre multicolor patterns. A surprise for mathematicians was the ability to generate very complex non-trivial structures using primitive algorithms.

As an example, consider the Mandelbrot set (see Fig. 3 and Fig. 4). The algorithm for its construction is quite simple and is based on a simple iterative expression:

Z = Z[i] * Z[i] + C,

where Zi and C are complex variables. Iterations are performed for each starting point C of a rectangular or square region - a subset of the complex plane. The iterative process continues until Z[i] goes beyond the circle of radius 2, the center of which lies at the point (0,0), (this means that the attractor of the dynamical system is at infinity), or after a sufficiently large number of iterations (for example 200-500) Z[i] will converge to some point on the circle. Depending on the number of iterations during which Z[i] remained inside the circle, you can set the color of point C (if Z[i] remains inside the circle for a sufficiently large number of iterations, the iteration process stops and this raster point is painted black) .

The above algorithm gives an approximation to the so-called Mandelbrot set. The Mandelbrot set contains points that do not go to infinity during an infinite number of iterations (points that are black). Points belonging to the boundary of the set (this is where complex structures arise) go to infinity in a finite number of iterations, and points lying outside the set go to infinity after several iterations (white background).

Examples of algebraic fractals:

Mandelbrot set
Julia sets
Halley's fractal
Newton's fractal

- 213.50 Kb

MINISTRY OF EDUCATION, SCIENCE, YOUTH AND SPORTS OF UKRAINE

ODESSA STATE ACADEMY OF CONSTRUCTION AND ARCHITECTURE

DEPARTMENT OF PHYSICS

ABSTRACT

Discipline: “Physical Materials Science”

On the topic: "FRACTALS"

Completed:

st. gr. ZPGS – 501 M

Zlunyaev E.A.

s/kn No. 08070

Checked:

Prof., Gerega A.N.

Odessa - 2013

FRACTALS

Introduction

1. What are fractals

2. Classic fractals

2.1 Koch's snowflake

2.2 Sierpinski's napkin and carpet

3. L-systems

4. Practical application of fractals

Literature

Introduction

When it seemed to most people that geometry in nature was limited to such simple figures as line, circle, conic section, polygon, sphere, quadratic surface, as well as their combinations. For example, what could be more beautiful than the statement that the planets in our solar system move around the sun in elliptical orbits?

However, many natural systems are so complex and irregular that using only familiar objects of classical geometry to model them seems hopeless. How, for example, can you build a model of a mountain range or a tree crown in terms of geometry? How to describe the diversity of biological configurations that we observe in the world of plants and animals? Imagine the complexity of the circulatory system, consisting of many capillaries and vessels and delivering blood to every cell of the human body. Imagine how cleverly the lungs and buds are arranged, reminiscent in structure of trees with a branched crown.

The dynamics of real natural systems can be just as complex and irregular. How to approach modeling cascading waterfalls or turbulent processes that determine weather?

Fractals and mathematical chaos are suitable tools for exploring these questions. The term fractal refers to some static geometric configuration, such as a snapshot of a waterfall. Chaos is a dynamical term used to describe phenomena similar to turbulent weather behavior. Often what we observe in nature intrigues us with the endless repetition of the same pattern, increased or decreased as many times as desired. For example, a tree has branches. On these branches there are smaller branches, etc. Theoretically, the branching element is repeated indefinitely, becoming smaller and smaller. The same thing can be seen when looking at a photograph of mountainous terrain. Try to zoom in a little on the mountain range - you will see the mountains again. This is how the property of self-similarity characteristic of fractals manifests itself.

Much work on fractals uses self-similarity as a defining property. Following Benoit Madelbrot, we accept the view that fractals should be defined in terms of fractal (fractional) dimension. This is where the origin of the word fractal comes from (from Latin fractus - fractional).

The concept of fractional dimension is a complex concept that is presented in several stages. A straight line is a one-dimensional object, while a plane is a two-dimensional object. If you twist the straight line and the plane well, you can increase the dimension of the resulting configuration; in this case, the new dimension will usually be fractional in some sense, which we have to clarify. The connection between fractional dimension and self-similarity is that with the help of self-similarity it is possible to construct a set of fractional dimension in the simplest way. Even in the case of much more complex fractals, such as the boundary of the Mandelbrot set, where there is no pure self-similarity, there is an almost complete repetition of the basic shape in an increasingly reduced form.

What are fractals

Fractals have been known for almost a century, are well studied and have numerous applications in life. This phenomenon is based very simple idea: an endless variety of shapes in beauty and variety can be obtained from relatively simple designs using just two operations - copying and scaling.

This concept does not have a strict definition. Therefore, the word "fractal" is not a mathematical term. This is usually the name given to a geometric figure that satisfies one or more of the following properties: has a complex structure at any magnification; is (approximately) self-similar; has a fractional Hausdorff (fractal) dimension, which is larger than the topological one; can be constructed by recursive procedures.

At the turn of the 19th and 20th centuries, the study of fractals was more episodic than systematic, because previously mathematicians mainly studied “good” objects that could be studied using general methods and theories. In 1872, the German mathematician Karl Weierstrass constructed an example of a continuous function that is nowhere differentiable. However, its construction was entirely abstract and difficult to understand. Therefore, in 1904, the Swede Helge von Koch came up with a continuous curve that has no tangent anywhere, and is quite easy to draw. It turned out that it has the properties of a fractal. One variant of this curve is called the “Koch snowflake”.

The ideas of self-similarity of figures were picked up by the Frenchman Paul Pierre Levy, the future mentor of Benoit Mandelbrot. In 1938, his article “Plane and spatial curves and surfaces consisting of parts similar to the whole” was published, which described another fractal - the Levy C-curve. All of these fractals listed above can be conditionally classified as one class of constructive (geometric) fractals. Another class is dynamic (algebraic) fractals, which include the Mandelbrot set. The first research in this direction dates back to the beginning of the 20th century and is associated with the names of the French mathematicians Gaston Julia and Pierre Fatou. In 1918, Julia published an almost two-hundred-page work on iterations of complex rational functions, which described Julia sets - a whole family of fractals closely related to the Mandelbrot set. This work was awarded a prize by the French Academy, but it did not contain a single illustration, so it was impossible to appreciate the beauty of the open objects. Despite the fact that this work made Julia famous among mathematicians of that time, it was quickly forgotten.

Attention again to the work of Julia and Fatou turned only half a century later, with the advent of computers: it was they who made visible the richness and beauty of the world of fractals. After all, Fatou could never look at the images that we now know as images of the Mandelbrot set, because the required number of calculations cannot be done by hand. The first person to use a computer for this was Benoit Mandelbrot.

In 1982, Mandelbrot’s book “Fractal Geometry of Nature” was published, in which the author collected and systematized almost all the information about fractals available at that time and presented it in an easy and accessible manner. Mandelbrot placed the main emphasis in his presentation not on heavy formulas and mathematical constructions, but on the geometric intuition of readers. Thanks to illustrations obtained using a computer and historical stories, with which the author skillfully diluted the scientific component of the monograph, the book became a bestseller, and fractals became known to the general public. Their success among non-mathematicians is largely due to the fact that, with the help of very simple designs and formulas that even a high school student can understand, the resulting images are amazing in complexity and beauty. When personal computers became powerful enough, even a whole direction in art appeared - fractal painting, and almost any computer owner could do it. Now on the Internet you can easily find many sites devoted to this topic.

1.1. Geometric (constructive) fractals

Fractals of this type are built in stages. First, the base is depicted. Then some parts of the base are replaced with a fragment. At each next stage, parts of the already constructed figure, similar to the replaced parts of the base, are again replaced with a fragment taken on a suitable scale. Each time the scale decreases. When the changes become visually unnoticeable, it is believed that the constructed figure approximates the fractal well and gives an idea of its shape. To obtain the fractal itself, an infinite number of stages are required. By changing the base and fragment, you can get many different geometric fractals.

Geometric fractals are good because, on the one hand, they are the subject of quite serious scientific study, and on the other hand, they can be “seen” - even a person far from mathematics will find something for themselves in them. This combination is rare in modern mathematics, where all objects are defined using obscure words and symbols. It turns out that many geometric fractals can be drawn literally on a piece of checkered paper. Let us immediately make a reservation that all the resulting images (including those shown on this poster) are only finite approximations of essentially infinite fractals. But you can always draw such an approximation that the eye will not distinguish very small details and our imagination will be able to create a correct picture of the fractal. For example, given a sufficiently large sheet of graph paper and some free time, you can manually draw such an accurate approximation of the Sierpinski carpet that from a distance of several meters the naked eye will perceive it as a real fractal. A computer will save time and paper and at the same time increase the accuracy of drawing.

Snowflake Koch

T-square; H-fractal

Sierpinski triangle

Tree of Pythagoras

Levy curve

1.2. Dynamic (algebraic) fractals

Mandelbrot set

Julia sets

Halley's fractal

Newton's fractal

2. Classic fractals

2.1 Koch's snowflake

At the beginning of the twentieth century, mathematicians were looking for curves that do not have a tangent at any point. This meant that the curve abruptly changed its direction, and at an enormously high speed (the derivative was equal to infinity). The search for these curves was not just caused by the idle interest of mathematicians. The fact is that at the beginning of the twentieth century quantum mechanics developed very rapidly. Researcher M. Brown sketched the trajectory of movement of suspended particles in water and explained this phenomenon as follows: randomly moving atoms of the liquid strike suspended particles and thereby set them in motion. After this explanation of Brownian motion, scientists were faced with the task of finding a curve that would best approximate the motion of Brownian particles. To do this, the curve had to meet the following properties: not have a tangent at any point. The mathematician Koch proposed one such curve. We will not go into explanations of the rules for its construction, but will simply present its image, from which everything will become clear (Fig. 1.1.1).

Figure 2.1.1. Snowflake Koch.

One important property, which the boundary of a Koch snowflake has - its infinite length. This may seem surprising because we are used to dealing with out-of-course curves mathematical analysis. Usually smooth or at least piecewise smooth curves always have a finite length (which can be verified by integration). Mandelbrot, in this regard, published a number of fascinating works that explore the question of measuring the length of the coastline of Great Britain. As a model he

Rice. 2.1.2. Construction of the Koch snowflake.

used a fractal curve, reminiscent of the edge of a snowflake, except that it introduced an element of randomness to take into account the randomness in nature. As a result, it turned out that the curve describing the coastline has an infinite length.

2.2 Sierpinski's napkin and carpet

Another example of a simple self-similar fractal is the Sierpinski napkin (Fig. 1.2.1), invented by the Polish mathematician Waclaw Sierpinski in 1915. The term napkin itself belongs to Mandelbrot. In the construction method below, we start with a certain region and sequentially eliminate internal subregions. Later we will consider other methods, in particular using L-systems, as well as based on iterated functions.

Figure 2.2.1. Sierpinski napkin

Let the initial set S0 be an equilateral triangle together with the region it encloses. Let us divide S0 into four smaller triangular regions, connecting the midpoints of the sides of the original triangle with segments. Let's remove the inside of the small central triangular area. Let's call the remaining set S1 (Fig. 1.2.2). We then repeat the process for each of the three remaining small triangles to obtain the next approximation S2. Continuing in this way, we obtain a sequence of nested sets Sn whose intersection is formed by the napkin S.

Rice. 2.2.2. Construction of a Sierpinski napkin

Obviously, the total area of the parts thrown out during construction is exactly equal to the area of the original triangle. In the first step we discarded ¼ of the area. In the next step, we threw out three triangles, each with an area equal to ¼ 2 of the area of the original one. Reasoning in this way, we are convinced that the total share of the discarded area was:

1/4 + 3*(1/42) + 32*(1/43) + … + 3n-1*(1/4n) + … .

This amount is equal. Therefore, we can claim that the remaining set S, that is, the napkin, has an area of measure zero. This makes S a “perfect” set, in the sense that it splits its complement into an infinite number of triangular regions, while having zero thickness.

Description of work

Butterflies, of course, know nothing about snakes. But birds that hunt butterflies know about them. Birds that do not recognize snakes well are more likely to...

If octo is Latin for “eight,” then why does an octave contain seven notes?

An octave is the interval between the two closest sounds of the same name: do and do, re and re, etc. From the point of view of physics, the “kinship” of these...

Why are important people called august?

In 27 BC. e. Roman Emperor Octavian received the title Augustus, which in Latin means “sacred” (in honor of the same figure, by the way...

What do they write in space?

A famous joke goes: “NASA spent several million dollars to develop a special pen that could write in space....

Why is the basis of life carbon?

About 10 million organic (that is, carbon-based) molecules and only about 100 thousand inorganic molecules are known. In addition...

Why are quartz lamps blue?

Unlike ordinary glass, quartz transmits ultraviolet light. IN quartz lamps The source of ultraviolet radiation is a gas discharge in mercury vapor. He...

Why does it sometimes rain and sometimes drizzle?

With a large temperature difference, powerful updrafts arise inside the cloud. Thanks to them, drops can stay in the air for a long time and...