An asymptote of the graph of a function y = f(x) is a straight line that has the property that the distance from the point (x, f(x)) to this straight line tends to zero as the graph point moves indefinitely from the origin.
In Figure 3.10. graphical examples of vertical, horizontal and oblique asymptotes are given.
Finding the asymptotes of the graph is based on the following three theorems.
Vertical asymptote theorem. Let the function y = f(x) be defined in a certain neighborhood of the point x 0 (possibly excluding this point itself) and at least one of the one-sided limits of the function is equal to infinity, i.e. Then the straight line x = x 0 is the vertical asymptote of the graph of the function y = f(x).
Obviously, the straight line x = x 0 cannot be a vertical asymptote if the function is continuous at the point x 0, since in this case 
. Consequently, vertical asymptotes should be sought at the discontinuity points of the function or at the ends of its domain of definition.
Horizontal asymptote theorem. Let the function y = f(x) be defined for sufficiently large x and there is a finite limit of the function. Then the line y = b is the horizontal asymptote of the graph of the function.
Comment. If only one of the limits is finite, then the function has, respectively, a left-sided or right-sided horizontal asymptote.
In the event that , the function may have an oblique asymptote.
Oblique asymptote theorem. Let the function y = f(x) be defined for sufficiently large x and there be finite limits 
. Then the straight line y = kx + b is the slanted asymptote of the graph of the function.
No proof.
An oblique asymptote, just like a horizontal one, can be right- or left-handed if the basis of the corresponding limits is infinity of a certain sign.
Studying functions and constructing their graphs usually includes next steps:
1. Find the domain of definition of the function.
2. Examine the function for even-odd parity.
3. Find vertical asymptotes by examining discontinuity points and the behavior of the function at the boundaries of the domain of definition, if they are finite.
4. Find horizontal or oblique asymptotes by examining the behavior of the function at infinity.
How to insert mathematical formulas on a website?
If you ever need to add one or two mathematical formulas to a web page, then the easiest way to do this is as described in the article: mathematical formulas are easily inserted onto the site in the form of pictures that are automatically generated by Wolfram Alpha. In addition to simplicity, this universal method will help improve the visibility of the site in search engines. It has been working for a long time (and, I think, will work forever), but is already morally outdated.
If you constantly use mathematical formulas on your site, then I recommend that you use MathJax - a special JavaScript library that displays mathematical notation in web browsers using MathML, LaTeX or ASCIIMathML markup.
There are two ways to start using MathJax: (1) using a simple code, you can quickly connect a MathJax script to your website, which will be automatically loaded from a remote server at the right time (list of servers); (2) download the MathJax script from a remote server to your server and connect it to all pages of your site. The second method - more complex and time-consuming - will speed up the loading of your site's pages, and if the parent MathJax server becomes temporarily unavailable for some reason, this will not affect your own site in any way. Despite these advantages, I chose the first method as it is simpler, faster and does not require technical skills. Follow my example, and in just 5 minutes you will be able to use all the features of MathJax on your site.
You can connect the MathJax library script from a remote server using two code options taken from the main MathJax website or on the documentation page:
One of these code options needs to be copied and pasted into the code of your web page, preferably between tags and or immediately after the tag. According to the first option, MathJax loads faster and slows down the page less. But the second option automatically monitors and loads the latest versions of MathJax. If you insert the first code, it will need to be updated periodically. If you insert the second code, the pages will load more slowly, but you will not need to constantly monitor MathJax updates.
The easiest way to connect MathJax is in Blogger or WordPress: in the site control panel, add a widget designed to insert third-party JavaScript code, copy the first or second version of the download code presented above into it, and place the widget closer to the beginning of the template (by the way, this is not at all necessary , since the MathJax script is loaded asynchronously). That's all. Now learn the markup syntax of MathML, LaTeX, and ASCIIMathML, and you are ready to insert mathematical formulas into your site's web pages.
Any fractal is constructed according to a certain rule, which is applied sequentially an unlimited number of times. Each such time is called an iteration.
The iterative algorithm for constructing a Menger sponge is quite simple: the original cube with side 1 is divided by planes parallel to its faces into 27 equal cubes. One central cube and 6 cubes adjacent to it along the faces are removed from it. The result is a set consisting of the remaining 20 smaller cubes. Doing the same with each of these cubes, we get a set consisting of 400 smaller cubes. Continuing this process endlessly, we get a Menger sponge.
Definition. An asymptote of the graph of a function is a straight line that has the property that the distance from a point on the graph of a function to this straight line tends to zero as the graph point moves indefinitely from the origin..
According to the methods of finding them, three types of asymptotes are distinguished: vertical, horizontal, oblique.
Obviously, horizontal ones are special cases of inclined ones (at ).
Finding the asymptotes of the graph of a function is based on the following statements.
Theorem 1. Let the function be defined at least in some semi-neighborhood of a point and at least one of its one-sided limits at this point is infinite, i.e. equalized. Then the straight line is the vertical asymptote of the graph of the function.
Thus, the vertical asymptotes of the graph of a function should be sought at the discontinuity points of the function or at the ends of its domain of definition (if these are finite numbers).
Theorem 2.
Let the function be defined for argument values sufficiently large in absolute value, and there is a finite limit of the function 
. Then the straight line is the horizontal asymptote of the graph of the function.
It may happen that 
, A 
, and are finite numbers, then the graph has two different horizontal asymptotes: left-handed and right-handed. If only one of the finite limits or exists, then the graph has either one left-handed or one right-handed horizontal asymptote.
Theorem 3.
Let the function be defined for values of the argument that are sufficiently large in absolute value, and there are finite limits 
And 
. Then the straight line is the oblique asymptote of the graph of the function.
Note that if at least one of these limits is infinite, then there is no oblique asymptote.
An oblique asymptote, like a horizontal one, can be one-sided.
Example. Find all asymptotes of the graph of the function.
Solution .
The function is defined at . Let us find its one-sided limits at points.
Because 
And 
(the other two one-sided limits may no longer be found), then the straight lines are vertical asymptotes of the graph of the function.
Let's calculate
(apply L'Hopital's rule) = 
.
This means that the straight line is a horizontal asymptote.
Since the horizontal asymptote exists, we are no longer looking for inclined ones (they don’t exist).
Answer: The graph has two vertical asymptotes and one horizontal.
General function research y = f(x).
The scope of the function. Find its domain of definition D(f) . If it's not too difficult, it's useful to also find the range E(f) . (However, in many cases, the question of finding E(f) is postponed until the extrema of the function are found.)
Special properties of the function. Find out the general properties of a function: evenness, oddness, periodicity, etc. Not every function has properties such as even or odd. A function is obviously neither even nor odd if its domain of definition is asymmetrical with respect to point 0 on the axis Ox. In the same way, for any periodic function the domain of definition consists either of the entire real axis or of the union of periodically repeating systems of intervals.
Vertical asymptotes. Find out how the function behaves when the argument approaches the boundary points of the domain of definition D(f), if such boundary points exist. In this case, vertical asymptotes may appear. If a function has discontinuity points at which it is not defined, then these points should also be checked for the presence of vertical asymptotes of the function.
Oblique and horizontal asymptotes. If the domain of definition D(f) includes rays of the form (a;+) or (−;b), then you can try to find oblique asymptotes (or horizontal asymptotes) for x+ or x−, respectively, i.e. find limxf(x). Oblique asymptotes: y = kx + b, where k=limx+xf(x) and b=limx+(f(x)−x). Asymptotes are horizontal: y = b, where limxf(x)=b.
Finding the intersection points of the graph with the axes. Finding the intersection point of the graph with the axis Oy. To do this you need to calculate the value f(0). Find also the points of intersection of the graph with the axis Ox, why find the roots of the equation f(x) = 0 (or make sure there are no roots). The equation can often be solved only approximately, but separating the roots helps to better understand the structure of the graph. Next, you need to determine the sign of the function on the intervals between the roots and breakpoints.
Finding the intersection points of the graph with the asymptote. In some cases, it may be necessary to find characteristic points of the graph that were not mentioned in the previous paragraphs. For example, if a function has a slanted asymptote, then you can try to find out if the graph has intersection points with this asymptote.
Finding intervals of convexity and concavity. This is done by examining the sign of the second derivative f(x). Find inflection points at the junctions of the convex and concave intervals. Calculate the value of the function at the inflection points. If a function has other points of continuity (except for inflection points) at which the second derivative is 0 or does not exist, then it is also useful to calculate the value of the function at these points. Having found f(x) we solve the inequality f(x)0. On each of the solution intervals the function will be convex downward. By solving the inverse inequality f(x)0, we find the intervals on which the function is convex upward (that is, concave). We define inflection points as those points at which the function changes direction of convexity (and is continuous).
The ghost of the asymptote has been wandering around the site for a long time to finally materialize in a separate article and bring particular delight to readers who are puzzled full study of the function. Finding the asymptotes of a graph is one of the few parts of this task that is covered in the school course only in an overview manner, since the events revolve around the calculation function limits, but they still relate to higher mathematics. For visitors who have little understanding of mathematical analysis, I think the hint is clear ;-) ...stop, stop, where are you going? Limits- it's easy!
Examples of asymptotes were encountered immediately in the first lesson about graphs of elementary functions, and the topic is now receiving detailed consideration.
So what is an asymptote?Imagine variable point, which “travels” along the graph of the function. Asymptote is straight, to whcih indefinitely close the graph of a function approaches as its variable point moves to infinity.
Note : definition is meaningful if you need formulation in notation mathematical analysis, please refer to the tutorial.
On the plane, asymptotes are classified according to their natural location:
1) Vertical asymptotes, which are given by an equation of the form , where “alpha” is a real number. A popular representative defines the ordinate axis itself,
with a slight feeling of nausea we remember the hyperbole.
2) Oblique asymptotes are traditionally written equation of a straight line With slope. Sometimes separate group allocate special case– horizontal asymptotes. For example, the same hyperbola with asymptote.
Let's go quickly, let's hit the topic with a short burst of machine gun fire:
How many asymptotes can the graph of a function have?Not one, one, two, three,... or infinitely many. We won’t go far for examples, let’s remember elementary functions. A parabola, a cubic parabola, and a sine wave do not have asymptotes at all. The graph of an exponential, logarithmic function has a single asymptote. The arctangent and arccotangent have two of them, and the tangent and cotangent have infinitely many. It is not uncommon for a graph to have both horizontal and vertical asymptotes. Hyperbole, will always love you.
What means ? Vertical asymptotes of the graph of a functionThe vertical asymptote of the graph is usually located at the point of infinite discontinuity functions. It’s simple: if a function has an infinite discontinuity at a point, then the straight line given by the equation is the vertical asymptote of the graph.
Note : Note that the entry is used to refer to two completely different concepts. Whether a point is implied or an equation of a line depends on the context.
Thus, to establish the presence of a vertical asymptote at a point, it is enough to show that at least one of the one-sided limits 
infinite. Most often this is the point where the denominator of the function is zero. Essentially, we have already found vertical asymptotes in recent examples lesson on the continuity of a function. But in some cases there is only one one-sided limit, and if it is infinite, then again - love and favor the vertical asymptote. The simplest illustration: and the ordinate axis (see. Graphs and properties of elementary functions
).
From the above, an obvious fact also follows: if the function is continuous on , then there are no vertical asymptotes. For some reason a parabola came to mind. Really, where can you “stick” a straight line here? ...yes... I understand... Uncle Freud's followers became hysterical =)
The converse statement is generally false: for example, the function is not defined on the entire number line, but is completely deprived of asymptotes.
Sloping asymptotes of the graph of a functionOblique (as a special case - horizontal) asymptotes can be drawn if the argument of the function tends to “plus infinity” or to “minus infinity”. Therefore, the graph of a function cannot have more than two slanted asymptotes. For example, the graph of an exponential function has a single horizontal asymptote at , and the graph of the arctangent at has two such asymptotes, and different ones at that.
When the graph in both places approaches a single oblique asymptote, then the “infinities” are usually combined under a single entry. For example, ...you guessed correctly: .
General rule of thumb :
If there are two final limit 
, then the straight line is the oblique asymptote of the graph of the function at . If at least one of the listed limits is infinite, then there is no oblique asymptote.
Note : the formulas remain valid if “x” tends only to “plus infinity” or only to “minus infinity”.
Let us show that the parabola has no oblique asymptotes: 
The limit is infinite, which means there is no oblique asymptote. Note that in finding the limit 
the need has disappeared since the answer has already been received.
Note
: If you have (or will have) difficulties understanding the plus-minus, minus-plus signs, please see the help at the beginning of the lesson
on infinitesimal functions, where I told you how to correctly interpret these signs.
It is obvious that any quadratic, cubic function, polynomial of the 4th and higher degrees also does not have oblique asymptotes.
Now let’s make sure that the graph also does not have an oblique asymptote. To reveal uncertainty we use L'Hopital's rule
:
, which was what needed to be checked.
When the function grows indefinitely, but there is no straight line to which its graph would approach infinitely close.
Let's move on to the practical part of the lesson:
How to find the asymptotes of the graph of a function?This is exactly how it is formulated typical task, and it involves finding ALL asymptotes of the graph (vertical, inclined/horizontal). Although, to be more precise in posing the question, we are talking about research for the presence of asymptotes (after all, there may not be any at all). Let's start with something simple:
Example 1
Find asymptotes of the graph of a function
The solution can be conveniently divided into two points:
1) First we check whether there are vertical asymptotes. The denominator goes to zero at , and it is immediately clear that at this point the function suffers endless gap, and the straight line given by the equation is the vertical asymptote of the graph of the function. But, before drawing such a conclusion, it is necessary to find one-sided limits: 
I remind you of the calculation technique that I similarly focused on in the article Continuity of function. Break points. In the expression under the limit sign we substitute . There's nothing interesting in the numerator:
.
But in the denominator it turns out infinitesimal a negative number
:
, it determines the fate of the limit.
The left-hand limit is infinite, and, in principle, it is already possible to make a verdict about the presence of a vertical asymptote. But one-sided limits are needed not only for this - they HELP TO UNDERSTAND HOW the graph of a function is located and to construct it CORRECTLY. Therefore, we must also calculate the right-handed limit: 
Conclusion: one-sided limits are infinite, which means that the straight line is the vertical asymptote of the graph of the function at .
First limit finite, which means it is necessary to “continue the conversation” and find the second limit:
The second limit too finite.
Thus, our asymptote is:
Conclusion: the straight line specified by the equation is the horizontal asymptote of the graph of the function at .
To find the horizontal asymptoteyou can use a simplified formula:
If exists finite limit, then the straight line is the horizontal asymptote of the graph of the function at .
It is easy to see that the numerator and denominator of the function same order of growth, which means the sought limit will be finite: 
Answer :
According to the condition, you do not need to complete the drawing, but if in full swing function study, then on the draft we immediately make a sketch: 
Based on the three found limits, try to figure out for yourself how the graph of the function might be located. Is it at all difficult? Find 5-6-7-8 points and mark them on the drawing. However, the graph of this function is constructed using transformations of the graph of an elementary function, and readers who carefully examined Example 21 of the above article can easily guess what kind of curve this is.
Example 2
Find asymptotes of the graph of a function
This is an example for independent decision. Let me remind you that it is convenient to divide the process into two points – vertical asymptotes and oblique asymptotes. In the sample solution, the horizontal asymptote is found using a simplified scheme.
In practice, fractional-rational functions are most often encountered, and after training on hyperbolas, we will complicate the task:
Example 3
Find asymptotes of the graph of a function 
Solution: One, two and done:
1) Vertical asymptotes are located at points of infinite discontinuity, so you need to check whether the denominator goes to zero. Let's decide quadratic equation
:
The discriminant is positive, so the equation has two real roots, and the work is significantly increased =) 
In order to further find one-sided limits quadratic trinomial It is convenient to factorize:
(for compact notation, the “minus” was included in the first bracket). To be on the safe side, let’s check by opening the brackets mentally or on a draft.
Let's rewrite the function in the form 
Let's find one-sided limits at the point: 
And at the point: 
Thus, the straight lines are vertical asymptotes of the graph of the function in question.
2) If you look at the function 
, then it is quite obvious that the limit will be finite and we have a horizontal asymptote. Let's show its presence in a short way: 
Thus, the straight line (abscissa axis) is the horizontal asymptote of the graph of this function.
Answer :
The found limits and asymptotes provide a lot of information about the graph of the function. Try to mentally imagine the drawing taking into account the following facts: 
Sketch your version of the graph on your draft.
Of course, the limits found do not clearly determine the appearance of the graph, and you may make a mistake, but the exercise itself will provide invaluable help during full function study. Correct picture- at the end of the lesson.
Example 4
Find asymptotes of the graph of a function
Example 5
Find asymptotes of the graph of a function 
These are tasks for independent solution. Both graphs again have horizontal asymptotes, which are immediately detected by the following features: in Example 4 growth order denominator more, than the order of growth of the numerator, and in Example 5 the numerator and denominator same order of growth. In the sample solution, the first function is examined for the presence of oblique asymptotes in full, and the second – through the limit.
Horizontal asymptotes, in my subjective impression, are noticeably more common than those that are “truly tilted.” The long-awaited general case:
Example 6
Find asymptotes of the graph of a function 
Solution: classic of the genre:
1) Since the denominator is positive, then the function continuous along the entire number line, and there are no vertical asymptotes. …Is it good? Not the right word - excellent! Point No. 1 is closed.
2) Let's check the presence of oblique asymptotes:
First limit finite, so let's move on. During the calculation of the second limit to eliminate uncertainty "infinity minus infinity" We bring the expression to a common denominator: 
The second limit too finite Therefore, the graph of the function in question has an oblique asymptote:
Conclusion :
Thus, when the graph of the function 
infinitely close approaches a straight line: 
Note that it intersects its oblique asymptote at the origin, and such intersection points are quite acceptable - it is important that “everything is normal” at infinity (in fact, this is where we are talking about asymptotes).
Example 7
Find asymptotes of the graph of a function
Solution: there is nothing special to comment on, so I will draw up an approximate example of a final solution:
1) Vertical asymptotes. Let's explore the point.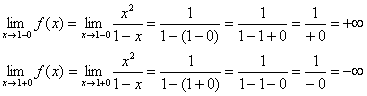 
The straight line is the vertical asymptote for the graph at .
2) Oblique asymptotes: 
The straight line is the slanted asymptote for the graph at .
Answer : 
The found one-sided limits and asymptotes allow us to predict with high confidence what the graph of this function looks like. Correct drawing at the end of the lesson.
Example 8
Find asymptotes of the graph of a function
This is an example for independent solution; for the convenience of calculating some limits, you can divide the numerator by the denominator term by term. Again, when analyzing your results, try to draw a graph of this function.
Obviously, the owners of “real” oblique asymptotes are the graphs of those fractional rational functions in which the leading degree of the numerator is one greater than the leading degree of the denominator. If it is more, there will be no oblique asymptote (for example, ).
But other miracles happen in life:
Example 9
Example 11
Examine the graph of a function for the presence of asymptotes
Solution: obviously 
, therefore we consider only the right half-plane, where there is a graph of the function.
Thus, the straight line (ordinate axis) is the vertical asymptote for the graph of the function at .
2) The study on oblique asymptote can be carried out according to the full scheme, but in the article L'Hopital's rules we found out that linear function higher order of growth than logarithmic, therefore: 
(See Example 1 of the same lesson).
Conclusion: the x-axis is the horizontal asymptote of the graph of the function at .
Answer :
, If ;
, If .
Drawing for clarity: 
It is interesting that a seemingly similar function has no asymptotes at all (those who wish can check this).
Two final examples for self-study:
Example 12
Examine the graph of a function for the presence of asymptotes 