1. It is possible to prove the statement that if a rectangular coordinate system OXYZ is given in space, then any equation of the first degree with three unknown x,y,z necessary and sufficiently defines a certain plane relative to this system R. This equation is called general plane equation and has next view:
A X+ B at+ C z+ D= 0 (17)
(compare with the general equation (15) of a straight line on a plane, which follows from this at z = 0) and defines the plane R, perpendicular to the vector (A,B,C).
Vector - normal vector of the plane R.
Equation (17) is equivalent to the following equations.
2. Equation of a plane passing through a given point M( x 0, y 0, z 0):
A( X- X 0) + B( at-at 0) + C( z-z 0) = 0.
3. Equation of a plane in segments
,
Where 
; 
; 
.
4. Equation of a plane passing through three given points, not lying on the same line, is written as a determinant
,
Where ( X 1 , y 1 , z 1), (X 2 , y 2 , z 2), (X 3 , y 3 , z 3) - coordinates of given points.
The angle between two planes is defined as the angle between their normal vectors n 1 and n 2. Hence the condition of parallel planes
R 1 and R 2:
and the condition of perpendicularity of two planes:
A 1 A 2 + B 1 IN 2 + C 1 WITH 2 = 0 .
Example 29. Through the point TO(1, -3, 2) draw a plane parallel to the vectors
a =(1, 2, -3) and b =(2,-1,-1) .
Solution. Let M ( X, at, z) – an arbitrary point of the desired plane. Vector
KM = (X- 1, at+ 3, z- 2) lies in this plane, and the vectors A And b parallel to it. Therefore, the vectors KM , a and b are coplanar. Then their mixed product is equal to zero:
.
Hence -(x –1) - (y + 3) – 5(z – 2) = 0 or x+ 7y + 5z + 10 = 0. This is the desired equation of the plane.
Different kinds equations of a line in space
A straight line in space can be specified as:
1) lines of intersection of two non-coinciding and non-parallel planes R 1 and R 2:
;
2) equations of a line passing through a given point M(X 0 , at 0 , z 0) in the direction specified by the vector L = (m, n, p):
,
which is called canonical equation of the line in space;
3) equations of a straight line passing through two given points M(X 1 , at 1 , z 1)
And M(x 2 , y 2 , z 2):
;
4) parametric equations:
.
Example 30. Reduce the equation of a straight line to canonical and parametric forms
.
Solution. A straight line is defined as the line of intersection of two planes. Normal vectors of these planes n 1 = (3,1,-2) and n 2 = (4,-7,-1) are perpendicular to the desired line, therefore their vector product [ n 1 , n 2 ] = L parallel to it is the vector [ n 1 , n 2 ] (or any collinear one) can be taken as a direction vector L the desired straight line.
[n 1 , n 2 ] = 
.
Let's take it as L = 3i + j + 5k. It remains to find some point on a given line. For this we put, for example, z = 0. We get
.
Having solved this system, we find X = 1, at= - 2. Thus, the point TO(1, -2, 0) belongs to a given line, and its canonical equation has the form
1. Types of equations of a straight line on a plane
| Name | Designation |
| General equation of a straight line on a plane | Ax + Bou + C = 0 perpendicular to the vector = (A, B) |
| Equation of a line in segments | Where a is the coordinate of the point of intersection of the line with the Ox axis, and b is the coordinate of the point of intersection of the line with the Oy axis. |
| Normal equation of a line | xcos j + ysin j - p = 0, p is the length of the perpendicular dropped from the origin to the straight line, and j is the angle formed by this perpendicular with the positive direction of the Ox axis. |
| Equation of a straight line with slope |
2. Basic problems on a straight line in space
| Task | Its implementation |
| The equation of a line passing through two points M 1 (x 1, y 1, z 1) and M 2 (x 2, y 2, z 2), |
|
| Angle between straight lines on a plane |
|
| Condition of perpendicularity and parallelism of lines | Two lines are parallel if k 1 = k 2. Two lines are perpendicular if |
| Distance from point M(x 0, y 0) to straight line Ah + Wu + C = 0 |
|
3. Types of plane equations in space
| Name | Designation |
| General plane equation | Ax + By + Cz + D = 0, where A, B, C are the coordinates of the vector |
| The equation of the plane passing through a given point M 0 (x 0, y 0, z 0) is perpendicular this vector(A, B, C) | A (x – x 0) + B (y – y 0) + C (z – z 0) = 0. |
| Equation of a plane in segments | The numbers a, b, c are the intersection points of the plane with the x, y, z axes, respectively. |
4. Basic problems on a plane in space
| Task | Its implementation |
| Equation of a plane passing through three points |
|
| Distance from point M 0 (x 0, y 0, z 0) to the plane Ах+Бу+Сz +D =0 |
|
| Angle between planes |
|
| Conditions for parallelism and perpendicularity of planes | Planes perpendicular If: . Planes, parallel, If |
5. Types of equations of a straight line in space
| Name | Designation |
| Parametric equations of a line | |
| Canonical equations of the line |
|
| General equations of a straight line in space |
|
, where (m, n, p) is the direction vector of the line, and M 0 (x 0, y 0, z 0) is the point through which the line passes.
, where the direction vector6. Basic problems on a straight line in space
| Task | Its implementation |
| Equation of a straight line in space, passing through two points M 1 (x 1, y 1, z 1) and M 2 (x 2, y 2, z 2) |
|
| Angle between straight lines in space |
|
| Conditions for parallelism and perpendicularity of lines in space | lines are parallel if the lines are perpendicular if . |
7. Basic problems on a plane and a line in space
8. Second order curves
| Name | Formula | Geometric interpretation |
| Ellipse |
|
|
| Circle |
|
|
| Hyperbola |
|
|
|
|
||
| Parabola | at 2 = 2px |
|
|
|
9. Second order surfaces
| Name | Formula | Geometric interpretation |
| sphere |
|
|
| elliptical cylinder |
|
|
| hyperbolic cylinder |
|
|
| parabolic cylinder |
|
|
| cone |
|
|
| ellipsoid |
|
|
| single-strip hyperboloid |
| |
| two-sheet hyperboloid |
|
|
| elliptical paraboloid |
|
|
| hyperbolic paraboloid |
|
or
In this module, the student must study theoretical material on the proposed educational elements. (cm. Theoretical material in higher mathematics: educational material for a student. Part I. Compiled by: Kalukova O.M., Kosheleva N.N., Nikitina M.G., Pavlova E.S., Emelyanova S.G. - Togliatti: TSU, 2005 and additional. literature)
Table 7 presents a schedule for studying theoretical material for the module “Analytical Geometry”
Table 7
| training | theoretical material |
|
| Auditory lessons | ||
| "The concept of the equation of a line on a plane" | ||
| "Plane and line in space" | Theoretical material on the topic "Elements of set theory" |
|
| "Second order curves" | Theoretical material on the topic "Elements of graph theory" |
|
| "Second order surfaces" | Theoretical material on the topic " Eigenvalues matrices" |
|
For any questions, contact an academic consultant by asking questions on the educational portal forum.
The student should also familiarize himself with typical tasks and module exercises to complete your version of the IPD (see Guide to solving problems: teaching aid for students Part I. Compiled by: Nikitina M.G., Pavlova E.S., - Togliatti: TSU, 2008.)
Table 8 shows the study schedule practical issues module "Analytical Geometry"
Table 8
| training | Practical lessons |
|
| Auditory lessons | independent work |
|
| Solving problems on the topic "Straight line on a plane" | ||
| Solving problems on the topic "Plane and line in space" | Solving problems on the topic "Elements of set theory" |
|
| Solving problems on the topic "Second order curves" | Solving problems on the topic "Elements of graph theory" |
|
| Solving problems on the topic "Second-order surfaces" | Solving problems on the topic "Eigenvalues of a matrix" |
|
For all questions, contact an academic consultant by asking questions on the educational portal forum or during individual consultation hours (the schedule of individual consultations is presented on the educational portal).
The student must complete his option homework(see Individual homework for students studying in 30/70 technology. Part I. Compiled by: Kalukova O.M., Kosheleva N.N., Nikitina M.G., Pavlova E.S., Emelyanova S.G. ., - Togliatti: TSU, 2005).
The implementation schedule is presented by the IDZ in Table 9.
Table 9
| Week of training | |
| from 1 to 4 task |
|
| from 5 to 7 task |
|
| from 8 to 11 task |
|
| 12.13 task |
At the end of the 12th week, pass the IDD to an academic consultant and receive admission to testing on the educational portal
On thirteenth week During training, students undergo module testing, which is set out in the schedule.
All equations of the plane, which are discussed in the following paragraphs, can be obtained from the general equation of the plane, and also reduced to general equation plane. Thus, when they talk about the equation of a plane, they mean the general equation of a plane, unless otherwise stated.
Equation of a plane in segments.
View plane equation 
, where a, b and c are non-zero real numbers, is called equation of the plane in segments.
This name is not accidental. Absolute values numbers a, b and c are equal to the lengths of the segments that the plane cuts off on the coordinate axes Ox, Oy and Oz, respectively, counting from the origin. The sign of the numbers a, b and c indicates in which direction (positive or negative) the segments should be plotted on the coordinate axes.
For example, let's build in rectangular system coordinates Oxyz plane defined by the equation of the plane in segments 
. To do this, mark a point that is 5 units away from the origin in the negative direction of the abscissa axis, 4 units in the negative direction of the ordinate axis, and 4 units in the positive direction of the applicate axis. All that remains is to connect these points with straight lines. The plane of the resulting triangle is the plane corresponding to the equation of the plane in segments of the form .
To get more complete information refer to the article equation of a plane in segments, it shows the reduction of the equation of a plane in segments to the general equation of a plane, there you will also find detailed solutions typical examples and tasks.
Normal plane equation.
The general plane equation of the form is called normal plane equation, If 
equal to one, that is, 
, And .
You can often see that the normal equation of a plane is written as . Here are the direction cosines of the normal vector of a given plane of unit length, that is, and p is a non-negative number equal to the distance from the origin to the plane.
The normal equation of a plane in the rectangular coordinate system Oxyz defines a plane that is removed from the origin by a distance p in the positive direction of the normal vector of this plane 
. If p=0, then the plane passes through the origin.
Let us give an example of a normal plane equation.
Let the plane be specified in the rectangular coordinate system Oxyz by the general equation of the plane of the form 
. This general equation of the plane is the normal equation of the plane. Indeed, the normal vector of this plane is 
has length equal to one, because 
.
The plane equation in normal form allows you to find the distance from a point to a plane.
We recommend that you understand this type of plane equation in more detail, look at detailed solutions to typical examples and problems, and also learn how to reduce the general plane equation to normal looking. You can do this by referring to the article.
Bibliography.
- Atanasyan L.S., Butuzov V.F., Kadomtsev S.B., Kiseleva L.S., Poznyak E.G. Geometry. Textbook for 10-11 grades of secondary school.
- Bugrov Ya.S., Nikolsky S.M. Higher mathematics. Volume one: elements of linear algebra and analytical geometry.
- Ilyin V.A., Poznyak E.G. Analytic geometry.
12.1. Basic Concepts
Surface and its equation
A surface in space can be considered as a locus of points that satisfy some condition. For example, a sphere of radius R with a center at point O 1 is the geometric locus of all points in space located at a distance R from point O 1.
The rectangular coordinate system Oxyz in space allows us to establish a one-to-one correspondence between points in space and triples of numbers x, y and z - their coordinates. A property common to all points on a surface can be written as an equation connecting the coordinates of all points on the surface.
The equation of a given surface in the rectangular coordinate system Oxyz is the equation F(x, y, z) = 0 with three variables x, y and z, which is satisfied by the coordinates of each point lying on the surface and not satisfied coordinates of points, not lying on this surface. The x, y, and z variables in the surface equation are called the current coordinates of the surface points.
The surface equation allows the study of the geometric properties of a surface to be replaced by the study of its equation. So, in order to find out whether a point M 1 (x 1 ;y 1 ;z 1) lies on a given surface, it is enough to substitute the coordinates of the point M 1 into the equation of the surface instead of variables: if these coordinates satisfy the equation, then the point lies on surfaces, if they do not satisfy, they do not lie.
Sphere equation
Let's find the equation of a sphere of radius R with center at point O 1 (x 0 ;y 0 ;z 0). According to the definition of a sphere, the distance of any of its points M(x; y; z) from the center O 1 (x 0 ;y 0 ;z 0) is equal to the radius R, i.e. O 1 M= R. But, where . Hence,
This is the required equation of the sphere. It is satisfied by the coordinates of any of its points and is not satisfied by the coordinates of points that do not lie on the given sphere.
If the center of the sphere Ο 1 coincides with the origin of coordinates, then the equation of the sphere takes the form .
If an equation of the form F(x;y;z) = 0 is given, then, generally speaking, it defines a certain surface in space.
The expression “generally speaking” means that in some cases the equation F(x; y; z) = 0 may not define a surface, but a point, a line, or not define any geometric image at all. They say “the surface degenerates.”
Thus, the equation is not satisfied by any real values of x, y, z. The equation is satisfied only by the coordinates of points lying on the Ox axis (from the equation it follows: y = 0, z = 0, and x is any number).
So, a surface in space can be defined geometrically and analytically. This leads to the formulation of two main tasks:
1. A surface is given as a locus of points. Find the equation of this surface.
2. Given the equation F(x;y;z) = 0. Investigate the shape of the surface defined by this equation.
Equations of a line in space
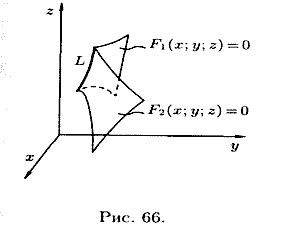
A line in space can be considered as the line of intersection of two surfaces (see Fig. 66) or as the locus of points common to two surfaces.
If 
And 
- equations of two surfaces defining line L, then the coordinates of the points of this line satisfy a system of two equations with three unknowns:
(12.1)
Comparisons of system (12.1) are called equations of a line in space. For example, there are equations for the Ox axis.
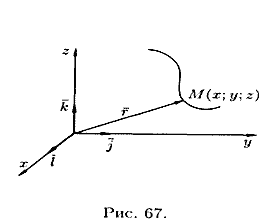
A line in space can be considered as the trajectory of a point (see Fig. 67). In this case, it is given by the vector equation
or parametric equations
projections of vector (12.2) on the coordinate axes.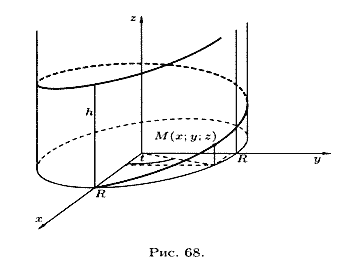 
For example, the parametric equations of a helix have the form
If point M moves uniformly along the generatrix of a circular cylinder, and the cylinder itself rotates uniformly around the axis, then point M describes a helical line (see Fig. 68).
12.2. Equations of a plane in space
The simplest surface is a plane. The plane in Oxyz space can be specified different ways. Each of them corresponds certain type her equations.
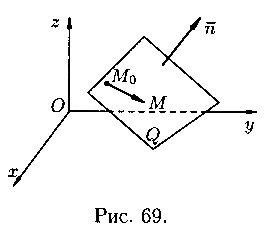
Equation of a plane passing through a given point perpendicular to a given vector
Let the plane Q in Oxyz space be defined by a point 
and vector perpendicular to this plane (see Fig. 69). Let us derive the equation of the plane Q. Take an arbitrary point on it and compose a vector. For any location of the point M on the plane Q, the vectors and are mutually perpendicular, therefore they scalar product equals zero: , i.e.
(12.3)
The coordinates of any point on the Q plane satisfy equation (12.3); the coordinates of points not lying on the Q plane do not satisfy this equation (for them ).
Equation (12.3) is called the equation of the plane passing through a given point perpendicular to the vector. It is of the first degree relative to the current coordinates x, y, z. The vector is called the normal vector of the plane.
Giving coefficients A, B and C to equation (12.3) different meanings, you can get the equation of any plane passing through the point . The set of planes passing through a given point is called a bundle of planes, and equation (12.3) is called the equation of a bundle of planes.
General plane equation
Consider a general first-degree equation with three variables x, y and z:
Assuming that at least one of the coefficients A, B or C is not equal to zero, for example, we rewrite equation (12.4) in the form
Comparing equation (12.5) with equation (12.3), we see that equations (12.4) and (12.5) are the equation of a plane with a normal vector passing through the point 
.
So, equation (12.4) defines a certain plane in the Oxyz coordinate system. Equation (12.4) is called the general equation of the plane.
Special cases of the general plane equation:
1. If D = 0, then it takes the form . This equation is satisfied by the point. Therefore, in this case the plane passes through the origin.
2. If C = 0, then we have the equation. The normal vector is perpendicular to the Οz axis. Consequently, the plane is parallel to the Οz axis; if B = 0 - parallel to the Oy axis, A = 0 - parallel to the Ox axis.
3. If C = D = 0, then the plane passes through parallel to the Οz axis, i.e., the plane passes through the Οz axis. Similarly, the equations correspond to planes passing through the Ox and Oy axes, respectively.
4. If A = B = 0, then equation (12.4) takes the form , i.e. The plane is parallel to the Oxy plane. Similarly, the equations and correspond to the plane, respectively parallel to planes Oyz and Οxz.
5. If A = B = D = 0, then equation (12.4) will take the form , i.e. z = 0. This is the equation of the Oxy plane. Similarly: y = 0 - equation of the Οxz plane; x = O - equation of the Oyz plane.
Equation of a plane passing through three given points
Three points in space that do not lie on the same straight line define a single plane. Let us find the equation of the plane Q passing through three given points M 1 (x 1 ;y 1 ;z 1), M 2 (x 2 ;y 2 ;z 2) and M 3 (x 3 ,y 3 ,z 3), not lying on the same straight line.
Let’s take an arbitrary point M(x;y;z) on the plane and compose the vectors , , . These vectors lie on the Q plane, therefore they are coplanar. We use the condition of coplanarity of three vectors (their mixed product is equal to zero), we obtain, i.e.
(12.6)
Equation (12.6) is the equation of a plane passing through three given points.
Equation of a plane in segments
Let the plane cut off the segments on the Ox, Oy and Oz axes, respectively a, b And c, i.e. passes through three points A(a;0;0), B(0;b;0) And C(0;0;c)(see Fig. 70). Substituting the coordinates of these points into equation (12.6), we obtain
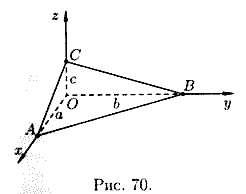
Expanding the determinant, we have , i.e., or
(12.7)
Equation (12.7) is called the equation of the plane in segments on the axes. It is convenient to use when constructing a plane.
Normal plane equation
The position of the plane Q is completely determined by specifying a unit vector having the direction of the perpendicular OK, lowered to
plane from the origin, and length p this perpendicular (see Fig. 71).
Let OK = p, and α, β, g are the angles formed by the unit vector е with the Ox, Oy and Οz axes. Then . Let's take an arbitrary point M(x; y; z) on the plane and connect it to the origin. Let's form a vector. For any position of the point M on the plane Q, the projection of the radius vector onto the direction of the vector is always equal to p:, i.e. or
(12.8)
Equation (12.8) is called the normal equation of the plane in vector form. Knowing the coordinates of the vectors f and e, we rewrite equation (12.8) in the form
Equation (12.9) is called the normal equation of the plane in coordinate form.
Note that the general plane equation (12.4) can be reduced to the normal equation (12.9) in the same way as was done for the equation of a line on a plane. Namely: multiply both sides of equation (12.4) by the normalizing factor 
, where the sign is taken opposite to the sign of the free term D of the general equation of the plane.
In the previous section devoted to the plane in space, we examined the issue from the perspective of geometry. Now let's move on to describing the plane using equations. A look at the plane from the side of algebra involves considering the main types of the equation of the plane in the rectangular coordinate system O x y z of three-dimensional space.
Yandex.RTB R-A-339285-1
Definition of the equation of a plane
Definition 1Plane- This geometric figure, consisting of individual points. Each point in three-dimensional space corresponds to coordinates that are specified by three numbers. The plane equation establishes the relationship between the coordinates of all points.
The equation of a plane in a rectangular coordinate system 0xz has the form of an equation with three variables x, y and z. The coordinates of any point lying within a given plane satisfy the equation; the coordinates of any other points that lie outside the given plane do not.
Substituting a point in a given plane into the equation of a coordinate plane turns the equation into an identity. When substituting the coordinates of a point lying outside the plane, the equation turns into an incorrect equality.
The plane equation can have several types. Depending on the specifics of the problems being solved, the plane equation can be written in different ways.
General plane equation
Let's formulate the theorem and then write down the equation of the plane.
Theorem 1
Any plane in a rectangular coordinate system O x y z in three-dimensional space can be specified by an equation of the form A x + B y + C z + D = 0, where A, B, C and D– some real numbers that are not equal to zero at the same time. Any equation of the form A x + B y + C z + D = 0 defines a plane in three-dimensional space
The equation of the form A x + B y + C z + D = 0 is called the general equation of the plane. If you don't attach numbers A, B, C And D specific values, then we obtain the equation of the plane in general form.
It is important to understand that the equation λ · A x + λ · B y + λ · C z + λ · D = 0 will define the plane in exactly the same way. In the equation, λ is some non-zero real number. This means that the equalities A x + B y + C z + D = 0 and λ · A x + λ · B y + λ · C z + λ · D = 0 are equivalent.
Example 1
The general equations of the plane x - 2 · y + 3 · z - 7 = 0 and - 2 · x + 4 · y - 2 3 · z + 14 = 0 are satisfied by the coordinates of the same points located in three-dimensional space. This means that they define the same plane.
Let us give an explanation of the theorem discussed above. A plane and its equation are inseparable, since each equation A x + B y + C z + D = 0 corresponds to a plane in a given rectangular coordinate system, and each plane located in three-dimensional space corresponds to its equation of the form A x + B y + C z + D = 0.
The plane equation A x + B y + C z + D = 0 can be complete or incomplete. All coefficients A, B, C and D in complete equation are different from zero. Otherwise, the general equation of the plane is considered incomplete.
Planes that are specified incomplete equations, can be parallel to the coordinate axes, pass through the coordinate axes, coincide with the coordinate planes or be located parallel to them, pass through the origin of coordinates.
Example 2
Consider the position in space of the plane given by the equation 4 · y - 5 · z + 1 = 0.
It is parallel to the x-axis and located perpendicular to the O y z plane. The equation z = 0 defines the coordinate plane O y z, and the general equation of the plane of the form 3 x - y + 2 z = 0 corresponds to the plane that passes through the origin.
Important clarification: coefficients A, B and C in the general equation of the plane represent the coordinates of the normal vector of the plane.
When they talk about the equation of a plane, they mean the general equation of a plane. All types of plane equations, which we will discuss in the next section of the article, are obtained from the general plane equation.
Normal plane equation
A normal plane equation is a general plane equation of the form A x + B y + C z + D = 0, which satisfies the following conditions: the length of the vector n → = (A, B, C) is equal to one, i.e. n → = A 2 + B 2 + C 2 = 1, and D ≤ 0.
Also, writing the normal equation of a plane can have the following form cos α · x + cos β · y + cos γ · z - p = 0, where p is a non-negative number that is equal to the distance from the origin to the plane, and cos α, cos β, cos γ are the direction cosines of the normal vector of a given plane of unit length.
n → = (cos α , cos β , cos γ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1
That is, according to the normal equation of the plane, the plane in the rectangular coordinate system O x y z is removed from the origin by a distance p in the positive direction of the normal vector of this plane n → = (cos α, cos β, cos γ). If p equals zero, then the plane passes through the origin.
Example 3
The plane is defined by a general plane equation of the form - 1 4 · x - 3 4 · y + 6 4 · z - 7 = 0. D = - 7 ≤ 0, the normal vector of this plane n → = - 1 4, - 3 4, 6 4 has a length equal to one, since n → = - 1 4 2 + - 3 4 2 + 6 4 = 1. Accordingly, this general plane equation is a normal plane equation.
For a more detailed study of the normal plane equation, we recommend going to the appropriate section. The topic provides analysis of problems and typical examples, as well as methods for bringing the general equation of a plane to normal form.
The plane cuts off segments of a certain length on the coordinate axes O x, O y and O z. The lengths of the segments are specified by non-zero real numbers a, b and c. The plane equation in segments has the form x a + y b + z c = 1. The sign of the numbers a, b and c shows in which direction from the zero value the segments on the coordinate axes should be plotted.
Example 4
Let us construct a plane in a rectangular coordinate system, which is specified by the equation of the plane formula in the segments x - 5 + y - 4 + z 4 = 1.
The points are removed from the origin in the negative direction by 5 units along the abscissa axis, by 4 units in the negative direction along the ordinate axis, and by 4 units in the positive direction along the applicate axis. Mark the points and connect them with straight lines.
The plane of the resulting triangle is the plane corresponding to the equation of the plane in segments, having the form x - 5 + y - 4 + z 4 = 1.
More detailed information about the equation of a plane in segments and bringing the equation of a plane in segments to the general equation of a plane is available in a separate article. There are also a number of solutions to problems and examples on the topic.
If you notice an error in the text, please highlight it and press Ctrl+Enter