Quadratic equation is an equation of the form ax 2 +bx +c = 0, where x– variable, a,b And c– some numbers, and a ≠ 0.
Example of a quadratic equation:
3x 2 + 2x – 5 = 0.
Here A = 3, b = 2, c = –5.
Numbers a,b And c– odds quadratic equation.
Number a called first coefficient, number b – second coefficient, and the number c – free member.
Reduced quadratic equation.
A quadratic equation in which the first coefficient is 1 is called given quadratic equation.
Examples of a given quadratic equation:
x 2 + 10x – 11 = 0
x 2 – x – 12 = 0
x 2 – 6X + 5 = 0
here is the coefficient at x 2 is equal to 1 (simply the 1 is omitted in all three equations).
Incomplete quadratic equation.
If in a quadratic equation ax 2 +bx +c = 0 at least one of the coefficients b or c is equal to zero, then such an equation is called incomplete quadratic equation.
Examples of incomplete quadratic equations:
2x 2 + 18 = 0
there is a coefficient here A, which is equal to -2, is the coefficient c, equal to 18, and the coefficient b no – it is equal to zero.
x 2 – 5x = 0
Here A = 1, b = -5, c= 0 (so the coefficient c missing from the equation).
How to solve quadratic equations.
To solve a quadratic equation, you need to perform only two steps:
1) Find the discriminant D using the formula:
D=b 2 – 4 ac.
If the discriminant is a negative number, then the quadratic equation has no solution, and the calculations stop. If D ≥ 0, then
2) Find the roots of the quadratic equation using the formula:
–
b ± √
D
X 1,2 = -----.
2A
Example: Solve quadratic equation 3 X 2 – 5X – 2 = 0.
Solution :
First, let's determine the coefficients of our equation:
A = 3, b = –5, c = –2.
We calculate the discriminant:
D= b 2 – 4ac= (–5) 2 – 4 3 (–2) = 25 + 24 = 49.
D > 0, which means the equation makes sense, which means we can continue.
Finding the roots of the quadratic equation:
–b+ √D 5 + 7 12
X 1 = ----- = ---- = -- = 2
2A 6 6
–b– √D 5 – 7 2 1
X 2 = ----- = ---- = – -- = – --.
2A 6 6 3
1
Answer : X 1 = 2, X 2 = – --.
Lesson summary
math teachers
MBOU Secondary School No. 2, Vorsma
Kiseleva Larisa Alekseevna
Topic: “Reduced quadratic equation. Vieta's theorem"
The purpose of the lesson: Introduction of the concept of a reduced quadratic equation, Vieta's theorem and its converse theorem.
Tasks:
Educational:
Introduce the concept of a reduced quadratic equation,
Derive the formula for the roots of the given quadratic equation,
Formulate and prove Vieta’s theorem,
Formulate and prove the theorem converse to Vieta’s theorem,
Teach students to solve the given quadratic equations using the theorem inverse to Vieta’s theorem.
Educational:
development logical thinking, memory, attention, general educational skills, abilities to compare and generalize;
Educational:
fostering hard work, mutual assistance, and mathematical culture.
Lesson type: lesson on introducing new material.
Equipment: algebra textbook ed. Alimova and others, notebook, handouts, presentation for the lesson.
Lesson plan.
Lesson stage
Content (goal) of the stage
Time (min)
Checking homework
Verification work
Analysis of work, answers to questions.
Learning new material
Formation of basic knowledge, formulation of rules, solving problems, analyzing results, answering student questions.
Mastering the studied material by applying it to solving problems by analogy under the supervision of a teacher.
Summing up the lesson
Assessing the knowledge of the students who responded. Testing knowledge and understanding of the wording of the rules using the frontal survey method.
Homework
Familiarize students with the content of the task and receive the necessary explanations.
Additional tasks
Multi-level tasks to ensure student development.
During the classes.
Organizing time. Setting the lesson goal. Creation favorable conditions For successful activities. Motivation for learning.
Checking homework. Frontal, individual testing and correction of students' knowledge and skills.
The equation
Number of roots
![]()
![]()
Teacher: How can you determine the number of its roots without solving a quadratic equation? (students' answers)
Verification work. Answers on questions.
Text test work:
Option #1.
Solve the equations:
A) ![]() ,
,
B) ![]()
![]() It has:
It has:
One root
Two different roots.
Option #2.
Solve the equations:
A) ![]() ,
,
B) ![]()
2.Find the value of parameter a for which the equation ![]() It has:
It has:
One root
Two different roots.
The test work is completed on separate sheets of paper and submitted to the teacher for checking.
After submitting the work, the solution is displayed on the screen.
Learning new material.
4.1. Francois Viet- French mathematician of the 16th century. He was a lawyer and later an adviser to the French kings Henry III and Henry II.
One day he managed to decipher a very complex Spanish letter intercepted by the French. The Inquisition almost burned him at the stake, accusing him of conspiring with the devil.
François Vieta is called the "father of modern letter algebra"
How are the roots connected? quadratic trinomial and its coefficients p and q? The answer to this question is given by a theorem that bears the name of the “father of algebra,” the French mathematician F. Vieta, which we will study today.
The famous theorem was published in 1591.
4.2. Let us formulate the definition of the reduced quadratic equation.
Definition. Quadratic equation of the form ![]() is called reduced.
is called reduced.
This means that the leading coefficient of the equation equal to one.
Example. .
Any quadratic equation ![]() can be reduced to the form
can be reduced to the form ![]() . To do this, you need to divide both sides of the equation by.
. To do this, you need to divide both sides of the equation by.
For example, the equation 7Х 2 – 12Х + 14 = 0 by dividing by 7 is reduced to the form
X 2 – 12/7X + 2 = 0
4.3. Derive formulas for the roots of the given quadratic equation.
![]()
![]()
a, b, c
a=1 , b=p , c=q
![]()
![]()
Solve the equation X 2 – 14X – 15 =0 (Student solves at the board)
Questions:
Name the coefficients p and q (-14, -15);
Write down the formula for the roots of the given quadratic equation;
Find the roots of this equation (X 1 = 15, X 2 = -1)
4.4. formulate and prove Vieta's theorem.
If and are the roots of the equation ![]() , then the formulas are valid, i.e. the sum of the roots of the reduced quadratic equation is equal to the second coefficient taken with the opposite sign, and the product of the roots is equal to the free term.
, then the formulas are valid, i.e. the sum of the roots of the reduced quadratic equation is equal to the second coefficient taken with the opposite sign, and the product of the roots is equal to the free term.
After this, the teacher proves the theorem. Then, together with the students, he draws a conclusion.
Example. ![]() . p =-5,q =6.
. p =-5,q =6.
So numbers and are numbers
positive. Need to find two positive numbers, whose product
equals 6, and the sum equals 5. =2, =3 are the roots of the equation.
4.5. Application of Vieta's theorem .
With its help you can:
Find the sum and product of the roots of a quadratic equation without solving it,
Knowing one of the roots, find another,
Identify signs roots of the equation,
Find the roots of an equation without solving it.
4.6. Let us formulate the theorem inverse to Vieta’s theorem.
If the numbers p, q, and are such that they satisfy the relations, then , are the roots of the quadratic equation ![]() .
.
The proof of the theorem converse to Vieta's theorem is taken home for strong students to study independently.
4.7. consider the solution to problem 5 on textbook page 125.
Reinforcing the material learned
№ 450 (1)
№ 451 (1, 3, 5) - orally
№ 452 (oral)
№ 455 (1,3)
№ 456 (1, 3)
Summing up the lesson.
Answer the questions:
State Vieta's theorem.

Why is Vieta's theorem needed?
State the converse of Vieta's theorem.
Homework.
§29 (before task 6), No. 450(2,4,6); 455(2.4); 456(2,4,6).
Additional tasks.
Level A.
Find the sum and product of the roots of the equation:

2. Using the inverse theorem of Vieta’s theorem, create a quadratic equation whose roots are 2 and 5.
Level B.
1.Find the sum and product of the roots of the equation:

2. Using the theorem inverse to Vieta’s theorem, create a quadratic equation whose roots are equal to and .
Level C.
1. Analyze the proof of the theorem converse to Vieta’s theorem
2. Solve the equation and check using the inverse theorem of Vieta’s theorem:


Lesson outline diagram
Stages of work
Contents of the stage
Organizing time, including:
setting a goal that must be achieved by students at this stage of the lesson (what must be done by students in order for them to further work was effective in the lesson)
description of methods for organizing students’ work on initial stage lesson, setting students up for educational activities, subject and topic of the lesson (taking into account real features class with which the teacher works)
The program requirements for the mathematical preparation of students on this topic is to introduce the concept of a reduced quadratic equation, Vieta's theorem and its inverse theorem (from the program for general education institutions).
8th grade students - children adolescence, which is characterized by instability of attention. The best way organize attention - organize learning activities in such a way that students have neither the time, nor the desire, nor the opportunity to be distracted for a long time.
Based on the above, the purpose of the lesson is to solve the following problems:
a) educational: introduction of the concept of a reduced quadratic equation, Vieta’s theorem and its converse theorem.
b) developing: development of logical thinking, memory, attention, general educational skills, abilities to compare and generalize;
c) educational: fostering hard work, mutual assistance, and mathematical culture.
In order for students to perceive the lesson as a logically complete, holistic, time-limited segment of the educational process, it begins with setting the rationale for the tasks and ends with summing up the results and setting tasks for the next lessons.
Survey of students on homework assignments, including:
determining the goals that the teacher sets for students at this stage of the lesson (what result should be achieved by students);
determining the goals and objectives that the teacher wants to achieve at this stage of the lesson;
description of methods that contribute to solving set goals and objectives;
description of the criteria for achieving the goals and objectives of this stage of the lesson;
determining possible actions of the teacher if he or the students fail to achieve their goals;
description of organization methods joint activities students, taking into account the characteristics of the class with which the teacher works;
description of methods of motivating (stimulating) students' learning activity during the survey;
description of methods and criteria for assessing student responses during the survey.
At the first stage, a frontal, individual check and correction of students’ knowledge and skills takes place. In this case, the solution is repeated quadratic equations and fixing the determination of the number of roots by its discriminant. The transition is made to the definition of the reduced quadratic equation.
At the second stage, equations of two types are considered. To prevent students from getting tired of monotonous work, they use various shapes work and task options, more tasks included high level(with parameter).
Students' oral work alternates with written work, which consists of justifying the choice of method for solving a quadratic equation and analyzing the solution to the equation
One of the methods of pedagogical support is the use of information technologies, which help students of different levels of preparedness to easily assimilate the material, therefore, certain moments of the lesson are conducted using a presentation (showing the solution independent work, questions, homework)
Learning new things educational material. This stage involves:
presentation of the main provisions of the new educational material that must be mastered by students;
description of forms and methods of presentation (presentation) of new educational material;
description of the main forms and methods of organizing individual and group activities of students, taking into account the characteristics of the class in which the teacher works;
a description of the criteria for determining the level of attention and interest of students in the educational material presented by the teacher;
description of methods of motivating (stimulating) students' educational activity during the development of new educational material
The definition of the reduced quadratic equation is given. The teacher, together with the students, deduces the formulas for the roots of the given quadratic equation, the students realize the importance of the educational material of the lesson. Analysis of the formulation and proof of Vieta’s theorem also occurs jointly with students
Such work is also a consolidation of the study of new material.
Methods:
visual;
practical;
verbal;
partial-search
Reinforcing educational material, suggesting:
setting a specific educational goal for students (what result should be achieved by students at this stage of the lesson);
determining the goals and objectives that the teacher sets for himself at this stage of the lesson;
description of forms and methods of achieving set goals during the consolidation of new educational material, taking into account individual characteristics students with whom the teacher works.
a description of the criteria to determine the degree to which students have mastered new educational material;
description possible ways and methods of responding to situations when the teacher determines that some students have not mastered the new educational material.
Reinforcement of educational material occurs when answering questions and working with the textbook:
Analysis of problem No. 5 on page 125;
Solution of exercises
№ 450 (1), 451 (1, 3, 5) – orally, 452 (orally);
455 (1,3); 456 (1, 3)
Throughout the lesson, students are highly active; the teacher has the opportunity to interview all students in the class, and some even more than once.
The lesson is summarized in the form of a frontal survey of students on the following questions:
What equations are called reduced?
Can an ordinary quadratic equation be reduced?
Write down the formula for the roots of the given quadratic equation
State Vieta's theorem.
What is the sum and product of the roots of the equation:
Homework assignment, including:
setting independent work goals for students (what students should do while completing homework);
determining the goals that the teacher wants to achieve by assigning homework;
defining and explaining to students the criteria for successfully completing homework.
IN homework Students are expected to work within their capabilities. Strong students work independently and at the end of the work have the opportunity to check the correctness of their solutions by checking them with the solutions written on the board at the beginning of the next lesson. Other students can get advice from their classmates or teacher. Weak students work based on examples and use solutions to equations discussed in class. Thus, conditions are created for working on various levels difficulties.
In this article we will look at solving incomplete quadratic equations.
But first, let’s repeat what equations are called quadratic. An equation of the form ax 2 + bx + c = 0, where x is a variable, and the coefficients a, b and c are some numbers, and a ≠ 0, is called square. As we see, the coefficient for x 2 is not equal to zero, and therefore the coefficients for x or the free term can be equal to zero, in which case we get an incomplete quadratic equation.
There are three types of incomplete quadratic equations:
1) If b = 0, c ≠ 0, then ax 2 + c = 0;
2) If b ≠ 0, c = 0, then ax 2 + bx = 0;
3) If b = 0, c = 0, then ax 2 = 0.
- Let's figure out how to solve equations of the form ax 2 + c = 0.
To solve the equation, move the free term from to right side equations, we get
ax 2 = ‒s. Since a ≠ 0, we divide both sides of the equation by a, then x 2 = ‒c/a.
If ‒с/а > 0, then the equation has two roots
x = ±√(–c/a) .
If ‒c/a< 0, то это уравнение решений не имеет. Более наглядно решение данных уравнений представлено на схеме.
Let's try to understand with examples how to solve such equations.
Example 1. Solve the equation 2x 2 ‒ 32 = 0.
Answer: x 1 = - 4, x 2 = 4.
Example 2. Solve the equation 2x 2 + 8 = 0.
Answer: the equation has no solutions.
- Let's figure out how to solve it equations of the form ax 2 + bx = 0.
To solve the equation ax 2 + bx = 0, let's factorize it, that is, take x out of brackets, we get x(ax + b) = 0. The product is equal to zero if at least one of the factors is equal to zero. Then either x = 0, or ax + b = 0. Solving the equation ax + b = 0, we get ax = - b, whence x = - b/a. An equation of the form ax 2 + bx = 0 always has two roots x 1 = 0 and x 2 = ‒ b/a. See what the solution to equations of this type looks like in the diagram. 
Let's consolidate our knowledge with a specific example.
Example 3. Solve the equation 3x 2 ‒ 12x = 0.
x(3x ‒ 12) = 0
x= 0 or 3x – 12 = 0
Answer: x 1 = 0, x 2 = 4.
- Equations of the third type ax 2 = 0 are solved very simply.
If ax 2 = 0, then x 2 = 0. The equation has two equal roots x 1 = 0, x 2 = 0.
For clarity, let's look at the diagram. 
Let us make sure when solving Example 4 that equations of this type can be solved very simply.
Example 4. Solve the equation 7x 2 = 0.
Answer: x 1, 2 = 0.
It is not always immediately clear what type of incomplete quadratic equation we have to solve. Consider the following example.
Example 5. Solve the equation

Let's multiply both sides of the equation by a common denominator, that is, by 30

Let's cut it down
5(5x 2 + 9) – 6(4x 2 – 9) = 90.
Let's open the brackets
25x 2 + 45 – 24x 2 + 54 = 90.
Let's give similar
Let's move 99 from the left side of the equation to the right, changing the sign to the opposite
Answer: no roots.
We looked at how incomplete quadratic equations are solved. I hope that now you will not have any difficulties with such tasks. Be careful when determining the type of incomplete quadratic equation, then you will succeed.
If you have questions on this topic, sign up for my lessons, we will solve the problems that arise together.
website, when copying material in full or in part, a link to the source is required.
Video tutorial 2: Solving Quadratic Equations
Lecture: Quadratic equations
The equation
The equation- this is a kind of equality in the expressions of which there is a variable.
Solve the equation- means finding a number instead of a variable that will bring it into correct equality.
An equation may have one solution, several, or none at all.
To solve any equation, it should be simplified as much as possible to the form:
Linear: a*x = b;
Square: a*x 2 + b*x + c = 0.
That is, any equations must be converted to standard form before solving.
Any equation can be solved in two ways: analytical and graphical.
On the graph, the solution to the equation is considered to be the points at which the graph intersects the OX axis.
Quadratic equations
An equation can be called quadratic if, when simplified, it takes the form:
a*x 2 + b*x + c = 0.
Wherein a, b, c are coefficients of the equation that differ from zero. A "X"- root of the equation. It is believed that a quadratic equation has two roots or may not have a solution at all. The resulting roots may be the same.
"A"- the coefficient that stands before the squared root.
"b"- stands before the unknown in the first degree.
"With" is the free term of the equation.
If, for example, we have an equation of the form:
2x 2 -5x+3=0
In it, “2” is the coefficient of the leading term of the equation, “-5” is the second coefficient, and “3” is the free term.
Solving a quadratic equation
There are a huge variety of ways to solve a quadratic equation. However, in a school mathematics course, the solution is studied using Vieta’s theorem, as well as using a discriminant.
Discriminant solution:
When solving using this method, it is necessary to calculate the discriminant using the formula:
![]()
If during calculations you find that the discriminant less than zero, this means that this equation has no solutions.
If the discriminant is zero, then the equation has two identical solutions. In this case, the polynomial can be collapsed using the abbreviated multiplication formula into the square of the sum or difference. Then solve it like linear equation. Or use the formula:
If the discriminant Above zero, then you need to use the following method:

Vieta's theorem
If the equation is given, that is, the coefficient of the leading term is equal to one, then you can use Vieta's theorem.
So let's assume the equation is:
The roots of the equation are found as follows:

Incomplete quadratic equation
There are several options for obtaining an incomplete quadratic equation, the form of which depends on the presence of coefficients.
1. If the second and third coefficients are zero (b = 0, c = 0), then the quadratic equation will look like:
This equation will have a unique solution. The equality will be true only if the solution to the equation is zero.
Quadratic equation - easy to solve! *Hereinafter referred to as “KU”. Friends, it would seem that there could be nothing simpler in mathematics than solving such an equation. But something told me that many people have problems with him. I decided to see how many on-demand impressions Yandex gives out per month. Here's what happened, look:

What does it mean? This means that about 70,000 people per month are searching for this information, what does this have to do with summer, and what will happen during the school year - there will be twice as many requests. This is not surprising, because those guys and girls who graduated from school a long time ago and are preparing for the Unified State Exam are looking for this information, and schoolchildren also strive to refresh their memory.
Despite the fact that there are a lot of sites that tell you how to solve this equation, I decided to also contribute and publish the material. Firstly, I want visitors to come to my site based on this request; secondly, in other articles, when the topic of “KU” comes up, I will provide a link to this article; thirdly, I’ll tell you a little more about his solution than is usually stated on other sites. Let's get started! The content of the article:
A quadratic equation is an equation of the form:

where coefficients a,band c are arbitrary numbers, with a≠0.
In the school course, the material is given in the following form– the equations are divided into three classes:
1. They have two roots.
2. *Have only one root.
3. They have no roots. It is worth especially noting here that they do not have real roots
How are roots calculated? Just!
We calculate the discriminant. Underneath this “terrible” word lies a very simple formula:
![]()
The root formulas are as follows:

*You need to know these formulas by heart.
You can immediately write down and solve:
Example:

1. If D > 0, then the equation has two roots.
2. If D = 0, then the equation has one root.
3. If D< 0, то уравнение не имеет действительных корней.
Let's look at the equation:

By on this occasion, when the discriminant is zero, the school course says that the result is one root, here it is equal to nine. Everything is correct, it is so, but...
This idea is somewhat incorrect. In fact, there are two roots. Yes, yes, don’t be surprised, you get two equal roots, and to be mathematically precise, then the answer should write two roots:
x 1 = 3 x 2 = 3
But this is so - a small digression. At school you can write it down and say that there is one root.
Now the next example:

As we know, the root of negative number is not extracted, so the solutions in in this case No.
That's the whole decision process.
Quadratic function.
This shows what the solution looks like geometrically. This is extremely important to understand (in the future, in one of the articles we will analyze in detail the solution to the quadratic inequality).
This is a function of the form:

where x and y are variables
a, b, c – given numbers, with a ≠ 0
The graph is a parabola:

That is, it turns out that by solving a quadratic equation with “y” equal to zero, we find the points of intersection of the parabola with the x axis. There can be two of these points (the discriminant is positive), one (the discriminant is zero) and none (the discriminant is negative). Details about quadratic function You can view article by Inna Feldman.
Let's look at examples:
Example 1: Solve 2x 2 +8 x–192=0
a=2 b=8 c= –192
D=b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Answer: x 1 = 8 x 2 = –12
*It was possible to immediately divide the left and right sides of the equation by 2, that is, simplify it. Calculations will be easier.
Example 2: Decide x 2–22 x+121 = 0
a=1 b=–22 c=121
D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

We found that x 1 = 11 and x 2 = 11
It is permissible to write x = 11 in the answer.
Answer: x = 11
Example 3: Decide x 2 –8x+72 = 0
a=1 b= –8 c=72
D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224
The discriminant is negative, there is no solution in real numbers.
Answer: no solution
The discriminant is negative. There is a solution!
Here we will talk about solving the equation in the case when a negative discriminant is obtained. Do you know anything about complex numbers? I will not go into detail here about why and where they arose and what their specific role and necessity in mathematics is; this is a topic for a large separate article.
The concept of a complex number.
A little theory.
A complex number z is a number of the form
z = a + bi
where a and b are real numbers, i is the so-called imaginary unit.
a+bi – this is a SINGLE NUMBER, not an addition.
The imaginary unit is equal to the root of minus one:

Now consider the equation:

We get two conjugate roots.
Incomplete quadratic equation.
Let's consider special cases, this is when the coefficient “b” or “c” is equal to zero (or both are equal to zero). They can be solved easily without any discriminatory issues.
Case 1. Coefficient b = 0.
The equation becomes:

Let's transform:
Example:
4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2
Case 2. Coefficient c = 0.
The equation becomes:

Let's transform and factorize:

*The product is equal to zero when at least one of the factors is equal to zero.
Example:
9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 or x–5 =0
x 1 = 0 x 2 = 5
Case 3. Coefficients b = 0 and c = 0.

Here it is clear that the solution to the equation will always be x = 0.
Useful properties and patterns of coefficients.
There are properties that allow you to solve equations with large coefficients.
Ax 2 + bx+ c=0 equality holds
a + b+ c = 0, That
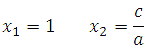
- if for the coefficients of the equation Ax 2 + bx+ c=0 equality holds
a+ s =b, That
![]()
These properties help to decide a certain type equations
Example 1: 5001 x 2 –4995 x – 6=0
The sum of the odds is 5001+( – 4995)+(– 6) = 0, which means

Example 2: 2501 x 2 +2507 x+6=0
Equality holds a+ s =b, Means

Regularities of coefficients.
1. If in the equation ax 2 + bx + c = 0 the coefficient “b” is equal to (a 2 +1), and the coefficient “c” is numerically equal to the coefficient “a”, then its roots are equal

ax 2 + (a 2 +1)∙x+ a= 0 = > x 1 = –a x 2 = –1/a.
Example. Consider the equation 6x 2 + 37x + 6 = 0.
x 1 = –6 x 2 = –1/6.
2. If in the equation ax 2 – bx + c = 0 the coefficient “b” is equal to (a 2 +1), and the coefficient “c” is numerically equal to the coefficient “a”, then its roots are equal

ax 2 – (a 2 +1)∙x+ a= 0 = > x 1 = a x 2 = 1/a.
Example. Consider the equation 15x 2 –226x +15 = 0.
x 1 = 15 x 2 = 1/15.
3. If in Eq. ax 2 + bx – c = 0 coefficient “b” is equal to (a 2 – 1), and coefficient “c” numerically equal to the coefficient “a”, then its roots are equal

ax 2 + (a 2 –1)∙x – a= 0 = > x 1 = – a x 2 = 1/a.
Example. Consider the equation 17x 2 +288x – 17 = 0.
x 1 = – 17 x 2 = 1/17.
4. If in the equation ax 2 – bx – c = 0 the coefficient “b” is equal to (a 2 – 1), and the coefficient c is numerically equal to the coefficient “a”, then its roots are equal

ax 2 – (a 2 –1)∙x – a= 0 = > x 1 = a x 2 = – 1/a.
Example. Consider the equation 10x 2 – 99x –10 = 0.
x 1 = 10 x 2 = – 1/10
Vieta's theorem.
Vieta's theorem is named after the famous French mathematician Francois Vieta. Using Vieta's theorem, we can express the sum and product of the roots of an arbitrary KU in terms of its coefficients.
45 = 1∙45 45 = 3∙15 45 = 5∙9.
In total, the number 14 gives only 5 and 9. These are roots. With a certain skill, using the presented theorem, you can solve many quadratic equations orally immediately.
Vieta's theorem, in addition. convenient in that after solving the quadratic equation in the usual way(through the discriminant) the resulting roots can be checked. I recommend doing this always.
TRANSPORTATION METHOD
With this method, the coefficient “a” is multiplied by the free term, as if “thrown” to it, which is why it is called "transfer" method. This method is used when the roots of the equation can be easily found using Vieta's theorem and, most importantly, when the discriminant is an exact square.
If A± b+c≠ 0, then the transfer technique is used, for example:
2X 2 – 11x+ 5 = 0 (1) => X 2 – 11x+ 10 = 0 (2)
Using Vieta's theorem in equation (2), it is easy to determine that x 1 = 10 x 2 = 1
The resulting roots of the equation must be divided by 2 (since the two were “thrown” from x 2), we get
x 1 = 5 x 2 = 0.5.
What is the rationale? Look what's happening.
The discriminants of equations (1) and (2) are equal:
If you look at the roots of the equations, you only get different denominators, and the result depends precisely on the coefficient of x 2:

The second (modified) one has roots that are 2 times larger.
Therefore, we divide the result by 2.
*If we reroll the three, we will divide the result by 3, etc.
Answer: x 1 = 5 x 2 = 0.5
Sq. ur-ie and Unified State Examination.
I’ll tell you briefly about its importance - YOU MUST BE ABLE TO DECIDE quickly and without thinking, you need to know the formulas of roots and discriminants by heart. Many problems included in the Unified State Examination tasks boil down to solving a quadratic equation (geometric ones included).
Something worth noting!
1. The form of writing an equation can be “implicit”. For example, the following entry is possible:
15+ 9x 2 - 45x = 0 or 15x+42+9x 2 - 45x=0 or 15 -5x+10x 2 = 0.
You need to bring him to standard view(so as not to get confused when deciding).
2. Remember that x is an unknown quantity and it can be denoted by any other letter - t, q, p, h and others.
