Fraktalna geometrija svijeta. Fraktalna geometrija je genetski kod Univerzuma

Sadržaj

Uvod

Koncept fraktala................................................. ........................................................4

Istorija pojavljivanja fraktala…………………………………………………………………….6

Algebarski fraktali………………………………………………………….8

Maldebrodski set……………………………………………...9
Julia set…………………………………………………………………11
Newtonovi bazeni (fraktali)……………………………………………………13
Fraktal (mjehurići) Halley………………………………………………………..14

Praktična upotreba fraktali……………………………………………...15

Zaključak……………………………………………………………………………………………….19

Spisak referenci…………………………………………………………………………………………20

Uvod

Jezik nauke se brzo menja u savremenom svetu. Istorija razvoja fizike seže više od jednog veka. Za to vrijeme proučavan je ogroman broj raznolikih prirodnih fenomena, otkriveni su fundamentalni zakoni fizike koji objašnjavaju različite eksperimentalne činjenice.

Većina sistema u prirodi kombinuje dva svojstva: prvo, oni su veoma veliki, često višestruki, raznoliki i složeni, i Drugo formiraju se pod uticajem vrlo malog broja jednostavnih zakona i dalje se razvijaju, poštujući te jednostavne zakone. Ovo je najviše različiti sistemi, počevši od kristala i jednostavno klastera (razne vrste klastera, kao što su oblaci, rijeke, planine, kontinenti, zvijezde), završavajući s ekosistemima i biološkim objektima (od lista paprati do ljudskog mozga). Fraktali su upravo takvi objekti: s jedne strane složeni (koji sadrže beskonačno mnogo elemenata), s druge strane, izgrađeni prema vrlo jednostavnim zakonima. Zahvaljujući ovom svojstvu, fraktali imaju mnogo zajedničkog sa mnogim prirodnim objektima. Ali fraktal ima prednost u poređenju sa prirodnim objektom po tome što fraktal ima strogu matematičku definiciju i podložan je strogom opisu i analizi. Stoga teorija fraktala omogućava predviđanje brzine rasta korijenskog sistema biljaka, troškova rada za isušivanje močvara, ovisnosti mase slame o visini izdanaka i još mnogo toga. Ovo je novi pravac u matematici, koji je napravio revoluciju u naučnoj paradigmi, uporediv po značaju sa teorijom relativnosti i kvantnom mehanikom. Objekti fraktalne geometrije na svoj način izgled oštro drugačiji od "pravilnih" geometrijskih oblika na koje smo navikli. U stvari, ovo je iskorak u matematičkom opisu sistema koji dugo vremena nisu bili pogodni za takav opis.

Fraktalna geometrija nije “čista” geometrijska teorija. To je prije koncept, novi pogled na dobro poznate stvari, restrukturiranje percepcije koje prisiljava istraživača da vidi svijet na novi način.

Svrha mog rada je da se upoznamo sa konceptom „fraktala“ i njegovom varijantom „algebarski fraktal“.

Fraktalni koncept

Relativno nedavno, u matematici se pojavila slika objekta, obimnija, ali ipak slična liniji. Nekim naučnicima je bilo teško da se pomire sa konceptom linije bez širine, pa su postepeno počeli da proučavaju geometrijski oblici i strukture koje imaju frakcionu prostornu dimenziju. Kontinuirane krivulje, koje imaju sve svoje derivate, zamijenjene su izlomljenim ili vrlo nazubljenim krivuljama. Upečatljiv primjer takve krive je putanja Brownove čestice. Tako je u nauci nastao koncept fraktala.

Fraktal(lat. fractus - zdrobljen, slomljen, slomljen) - složena geometrijska figura koja ima svojstvo samosličnosti, odnosno sastavljena od nekoliko dijelova, od kojih je svaki sličan cijeloj figuri (slika 1). U širem smislu, fraktali se shvataju kao skupovi tačaka u euklidskom prostoru koji imaju razlomačnu metričku dimenziju (u smislu Minkowskog ili Hausdorffa) ili metričku dimenziju.

Rice. 1
Treba napomenuti da riječ „fraktal“ nije matematički termin i nema općeprihvaćenu strogu matematičku definiciju. Može se koristiti kada dotična figura ima bilo koje od sljedećih svojstava:

Ima netrivijalnu strukturu na svim skalama. Ovo je u suprotnosti sa regularnim figurama (kao što su krug, elipsa, graf glatka funkcija): Ako pogledamo mali fragment pravilne figure u vrlo velikom mjerilu, izgledat će kao fragment prave linije. Za fraktal, povećanje skale ne dovodi do pojednostavljenja strukture; na svim skalama ćemo vidjeti jednako složenu sliku.

Je li sebi sličan ili približno sebi sličan.

Ima frakcijsku metričku dimenziju.

Mnogi objekti u prirodi imaju fraktalna svojstva, na primjer, obale, oblaci, krošnje drveća, cirkulacijski sistem i alveolarni sistem ljudi ili životinja.
Fraktali, posebno u avionu, popularni su zbog kombinacije ljepote s lakoćom konstrukcije pomoću kompjutera.

Istorija fraktala

Proučavanje fraktala na prelazu iz 19. u 20. vek bilo je više epizodično nego sistematično, jer su matematičari ranije uglavnom proučavali „dobre“ objekte koji su se mogli proučavati pomoću uobičajene metode i teorije. Njemački matematičar Karl Weierstrass je 1872. godine konstruirao primjer neprekidne funkcije koja se nigdje ne može razlikovati, odnosno nema tangentu ni u jednoj tački. Međutim, njegova konstrukcija je bila potpuno apstraktna i teško razumljiva. Stoga je 1904. Šveđanin Helge von Koch osmislio kontinuiranu krivu koja nigdje nema tangente i koju je prilično lako nacrtati. Ispostavilo se da ima svojstva fraktala. Jedna varijanta ove krive se zove “Koch pahulja”.
Ideje o samosličnosti figura preuzeo je Francuz Paul Pierre Levy, budući mentor Benoita Mandelbrota. Godine 1938. objavljen je njegov članak "Ravne i prostorne krive i površine koje se sastoje od dijelova sličnih cjelini", u kojem je opisan još jedan fraktal - Levyjeva C-kriva. Svi ovi gore navedeni fraktali mogu se uslovno svrstati u jednu klasu konstruktivnih (geometrijskih) fraktala.
Druga klasa su dinamički (algebarski) fraktali, koji uključuju Mandelbrotov skup. Prva istraživanja u ovom pravcu započela su početkom 20. veka i vezuju se za imena francuskih matematičara Gastona Julije i Pjera Fatua. Godine 1918, Julijin rad je objavljen o iteracijama kompleksa racionalne funkcije, koji opisuje Julia skupove, čitavu porodicu fraktala blisko povezanih sa Mandelbrotovim skupom. Ovaj rad je dobio nagradu Francuske akademije, ali nije sadržavao niti jednu ilustraciju, pa je bilo nemoguće cijeniti ljepotu otvorenih objekata

Prve ideje fraktalne geometrije nastale su u 19. veku. Cantor je, koristeći jednostavnu rekurzivnu (ponavljajuću) proceduru, pretvorio liniju u kolekciju nepovezanih tačaka (tzv. Cantorova prašina). Uzeo bi liniju i uklonio središnju trećinu, a zatim bi ponovio isto sa preostalim dijelovima. (sl. 2)

Rice. 2

Peano je povukao posebnu vrstu linije (slika 3)

Rice. 3

Da bi ga nacrtao, Peano je koristio sljedeći algoritam.

U prvom koraku uzeo je ravnu liniju i zamijenio je sa 9 segmenata 3 puta kraćih od dužine originalne linije (1. i 2. dio slike). Zatim je učinio isto sa svakim segmentom rezultirajuće linije. I tako redom do beskonačnosti. Jedinstvenost linije je u tome što ispunjava čitavu ravan. Dokazano je da se za svaku tačku na ravni može naći tačka koja pripada Peanovoj pravoj.

Peanova kriva i Cantorova prašina prevazišli su obične geometrijske objekte. Nisu imali jasnu dimenziju. Činilo se da je Kantorova prašina izgrađena na osnovu jednodimenzionalne prave linije, ali se sastojala od tačaka (dimenzija 0). A Peano kriva je izgrađena na osnovu jednodimenzionalne linije, a rezultat je bila ravan. U mnogim drugim oblastima nauke pojavili su se problemi čije je rešavanje dovelo do čudnih rezultata sličnih gore opisanim (Brownovsko kretanje, cene akcija).

Sve do 20. stoljeća prikupljali su se podaci o takvim čudnim objektima, bez ikakvog pokušaja da se oni sistematiziraju. To je bilo sve dok ih nije preuzeo Benoit Mandelbrot, otac moderne fraktalne geometrije i riječi fraktal. Postepeno uspoređujući činjenice, došao je do otkrića novog smjera u matematici - fraktalne geometrije.

Da bismo jasnije zamislili fraktal, razmotrimo primjer dat u knjizi B. Mandelbrota "Fraktalna geometrija prirode", koja je postala klasična - "Kolika je dužina obale Britanije?" Odgovor na ovo pitanje nije tako jednostavan kao što se čini. Sve ovisi o dužini alata koji se koristi. Mjerenjem obale pomoću kilometrskog ravnala, dobiju određenu dužinu. Međutim, promašene su mnoge male uvale i poluostrva, koja su mnogo manja od izmjerenog vladara. Smanjenjem veličine ravnala na 1 metar, ispada da će dužina obale postati duža. Prilikom mjerenja dužine bankine pomoću milimetarskog ravnala, uzimajući u obzir dijelove koji su veći od milimetra, dužina će biti još veća. Kao rezultat toga, odgovor na tako naizgled jednostavno pitanje može svakoga zbuniti - dužina britanske obale je beskrajna.

Algebarski fraktali

Algebarski fraktali su dobili ime jer su izgrađeni na osnovu algebarskih formula. Postoji nekoliko metoda za dobijanje algebarskih fraktala. Jedna od metoda je da se više puta izračunava funkcija gdjez - kompleksni broj, a f je određena funkcija. Izračunavanje ove funkcije se nastavlja sve dok se ne ispuni određeni uvjet. A kada je ovaj uslov ispunjen, na ekranu se prikazuje tačka. U ovom slučaju, vrijednosti funkcije za različite točke kompleksne ravni mogu imati različito ponašanje:

teži ka beskonačnosti tokom vremena;

teži 0;
uzima nekoliko fiksnih vrijednosti i ne prelazi ih;
ponašanje je haotično, bez ikakvih trendova.

3.1 Mandelbrotov set

Mandelbrotov skup (jedan od najpoznatijih fraktalnih objekata) prvi je konstruisao (vizuelno pomoću kompjutera) Benoit Mandelbrot u proleće 1980. godine u IBM istraživačkom centru. Thomas J. Watson. I iako su istraživanja ovakvih objekata počela još u prošlom stoljeću, upravo je otkriće ovog skupa i poboljšanje hardvera kompjuterske grafike presudno utjecalo na razvoj fraktalne geometrije i teorije haosa. Dakle, šta je Mandelbrotov skup?

Razmotrimo funkciju kompleksne varijable. Hajde da stavimoi razmotrite redosled, gdje za bilo. Takav niz može biti ograničen (tj. može postojati r takvo da za bilo koje) ili “bježi u beskonačnost” (tj. za bilo koje r > 0 postoji). Mandelbrotov skup se može definirati kao skup kompleksnih brojeva c za koje je navedeni niz ograničen. Nažalost, ne postoji poznati analitički izraz koji bi omogućio dato c da odredi da li pripada Mandelbrotovom skupu ili ne. Stoga se za konstruiranje skupa koristi kompjuterski eksperiment: oni gledaju kroz skup tačaka na kompleksnoj ravni sa određenim korakom i za svaku tačku izvode određeni broj iteracije (pronaći određeni broj članova niza) i pratiti njegovo „ponašanje“. (Sl. 4).

Dokazano je da se Mandelbrotov skup nalazi u krugu poluprečnika r=2 sa središtem u početku. Dakle, ako u nekom koraku modul sljedećeg člana niza prelazi 2, možemo odmah zaključiti da tačka koja odgovara c, koja definira ovaj niz, ne pripada Mandelbrotovom skupu.

Smanjenjem koraka na kojem se skeniraju kompleksni brojevi i povećanjem broja iteracija, možemo dobiti onoliko detaljne koliko želimo, ali uvijek samo približne slike skupa.

Neka nam je na raspolaganju N boja, numerisanih za određenost od 0 do N-1. Pretpostavićemo, opet radi određenosti, da crna boja ima broj 0. Ako za dato c nakon N-1 iteracija tačka ne ide dalje od kruga poluprečnika 2, pretpostavićemo da c pripada Mandelbrotovom skupu i oslikati ovo tačka c crna. U suprotnom, ako je u nekom koraku k (k Ê ) sljedeća tačka izašla izvan kruga poluprečnika 2 (tj. u k-tom koraku smo shvatili da “bježi”), obojite je bojom k.

Prekrasne slike dobijaju se uspješnim izborom palete i susjedstva skupa (naime, izvan seta ćemo dobiti „tačke u boji“) (sl. 5, 6).

Rice. 4

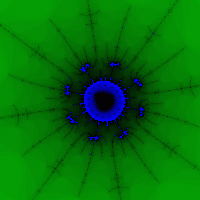
Rice. 5 Fig. 6

3.2 Julia set

Julijine skupove, blisko povezane sa Mandelbrotovim skupom, proučavali su početkom 20. veka matematičari Gaston Julia i Pierre Fatou (vidi). Godine 1917-1919 dobili su fundamentalne rezultate vezane za iteraciju funkcija kompleksne varijable. Uopšteno govoreći, ova činjenica zaslužuje posebnu raspravu i predstavlja impresivan primjer matematičkog istraživanja, mnogo desetljeća ispred svog vremena (naučnici su mogli samo približno zamisliti kako su izgledali objekti koje su proučavali!), ali ćemo opisati samo metodu za konstruiranje Julije skupovi za funkciju kompleksne varijable. Tačnije, gradićemo tzv. "puniti Julia setove".

Razmotrimo pravougaonik (x 1 ;y 1 )-(x 2 ;y 2 ). Popravimo konstantu c i počnemo da gledamo tačke izabranog pravougaonika sa određenim korakom. Za svaku tačku, kao kod konstruisanja Mandelbrotovog skupa, izvršićemo seriju iteracija (što je veći broj iteracija, to će skup biti tačniji). Ako nakon niza iteracija tačka ne “pobjegne” izvan granice kruga poluprečnika 2, obojićemo je crnom bojom, inače bojom iz palete. (sl. 7, 8, 9, 10).

Rice. 7

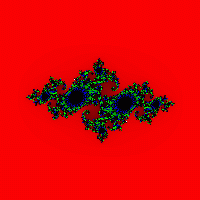
Fig.8 Sl. 9

Rice. 10

3.3 Newtonovi bazeni (fraktali)

Druga vrsta dinamičkih fraktala su Njutnovi fraktali (tzv. baseni). (Sl. 11). Formule za njihovu konstrukciju zasnovane su na metodi rješavanja nelinearnih jednačina, koju je izumio veliki matematičar još u 17. vijeku. Primjena opšta formula Newtonovom metodom zn+1 = zn - f (zn)/f"(zn), n=0, 1, 2… da riješimo jednačinu f (x)=0 na polinom zk-a, dobijamo niz tačaka : zn+1 = (k-1)znk/kznk-1, n=0, 1, 2... Odabirom raznih kompleksnih brojeva z0 kao početnih aproksimacija, dobićemo nizove koji konvergiraju korijenima ovog polinoma. ima tačno k korijena, tada je cijela ravan podijeljena na k dijelova - područja privlačenja korijena. Granice ovih dijelova imaju fraktalnu strukturu.

Rice. jedanaest

3.4 Fraktal (mjehurići) Halley

Takvi fraktali se dobijaju ako se po pravilu za konstruisanje dinamičkog fraktala koristi Halejeva formula za pronalaženje približnih vrednosti korena funkcije. (Sl. 12).

Metoda se sastoji od niza iteracija:

Ideja metode je skoro ista kao ona koja se koristi za crtanje dinamičkih fraktala: uzimamo neku početnu vrijednost (kao i obično, ovdje govorimo o vrijednosti varijabli i funkcija) i primijeniti formulu na nju mnogo puta, dobivajući niz brojeva. Gotovo uvijek konvergira jednoj od nula funkcije (to jest, vrijednosti varijable na kojoj funkcija uzima vrijednost 0). Halejeva metoda, uprkos glomaznoj formuli, radi efikasniji od metode : Slijed brže konvergira na nultu funkciju.

Rice. 12

Praktična primjena fraktala

Fraktali se sve više koriste u nauci. Glavni razlog za to je taj što opisuju stvarnom svijetu ponekad čak i bolje od tradicionalne fizike ili matematike. Evo nekoliko primjera.

Računarski sistemi

Od svih slika koje kompjuter može stvoriti, malo njih može parirati fraktalnim slikama kada je u pitanju prava ljepota.

Većina korisna upotreba Fraktali u informatici su fraktalna kompresija podataka. Ova vrsta kompresije je zasnovana na činjenici da je stvarni svijet dobro opisan fraktalnom geometrijom. Istovremeno, slike se kompresuju mnogo bolje nego što se to radi konvencionalnim metodama (kao što su jpeg ili gif). Još jedna prednost fraktalne kompresije je da kada se slika uveća, nema efekta pikselizacije (povećanje veličine tačaka do veličina koje iskrivljuju sliku). Sa fraktalnom kompresijom, nakon povećanja, slika često izgleda čak i bolje nego prije.

Mehanika fluida

Proučavanje turbulencije u strujanjima je vrlo dobro prilagođeno

fraktali. Turbulentni tokovi su haotični i stoga ih je teško precizno modelirati. I tu pomaže prijelaz na fraktalni prikaz, što uvelike olakšava rad inženjera i fizičara, omogućavajući im da bolje razumiju dinamiku složenih tokova.

Koristeći fraktale također možete simulirati plamen.

Porozni materijali su dobro zastupljeni u fraktalnom obliku zbog činjenice da imaju vrlo složenu geometriju. Koristi se u nauci o nafti.

Telekomunikacije

Za prijenos podataka na daljinu, antene sa

fraktalnih oblika, što uvelike smanjuje njihovu veličinu i težinu. Fraktali se koriste za opisivanje zakrivljenosti površina. Neravnu površinu karakterizira kombinacija dva različita fraktala.
Lijek

Biosenzorne interakcije. Otkucaj srca.
Biologija

Modeliranje haotičnih procesa, posebno kada se opisuju modeli populacije.
Nanotehnologija

U slučaju nanotehnologije, fraktali također igraju ulogu važnu ulogu, budući da, zbog svoje hijerarhijske samoorganizacije, mnogi nanosistemi imaju necjelobrojnu dimenziju, odnosno fraktali su po svojoj geometrijskoj, fizičko-hemijskoj ili funkcionalnoj prirodi. Na primjer, upečatljiv primjer hemijskih fraktalnih sistema su molekule "dendrimeri » . (Sl. 13)

Rice. 13

Književnost

Među književna djela pronađite one koji imaju tekstualnu, strukturnu ili semantičku fraktalnu prirodu. U tekstualnim fraktalima elementi teksta se potencijalno beskonačno ponavljaju (“Sveštenik je imao psa...”, “Parbola o filozofu koji sanja da je on leptir koji sanja da je ona filozof koji sanja...” i tekstovi sa ekstenzijama ("Kuća koju je sagradio Jack")

U strukturalnim fraktalima, shema teksta je potencijalno fraktalna: vijenac od soneta (15 pjesama), vijenac od vijenaca soneta (211 pjesama), vijenac od vijenaca od soneta (2455 pjesama).

Zaključak

Fraktal je objekat beskonačne složenosti, koji vam omogućava da vidite što više njegovih detalja izbliza kao i izdaleka. Zemlja je klasičan primjer fraktalnog objekta. Iz svemira izgleda kao lopta. Ako mu se približimo, naći ćemo okeane, kontinente, obale i planinske lance. Pogledajmo planine izbliza - još finiji detalji će postati vidljivi: komad zemlje na površini planine, po svojoj veličini, složen je i neravan kao i sama planina. A još veće povećanje će otkriti sitne čestice tla, od kojih je svaka sama po sebi fraktalni objekt.

U zaključku, želim reći da je nakon što su fraktali otkriveni mnogim naučnicima postalo očigledno da su stari dobri oblici euklidske geometrije mnogo inferiorniji od većine prirodnih objekata zbog nedostatka neke nepravilnosti, nereda i nepredvidivosti u njima. Moguće je da će nove ideje fraktalne geometrije pomoći u proučavanju mnogih misterioznih fenomena okolna priroda. Trenutno, fraktali ubrzano osvajaju mnoga područja fizike, biologije, medicine, sociologije i ekonomije. Metode obrade slika i prepoznavanja uzoraka koje koriste nove koncepte omogućavaju istraživačima da koriste ovaj matematički aparat za kvantitativno opisivanje ogromnog broja prirodnih objekata i struktura.

Bibliografija

1. Uvod u fraktale,

2. Žikov V.V. O setovima Julije. // Moderna prirodna nauka: Enciklopedija: U 10 tomova T.1: Matematika. Mehanika. M., 2000.

3. Žikov V.V. Fraktali. // Moderne prirodne nauke: Enciklopedija: U 10 tomova T.1: Matematika. Mehanika. M., 2000.

4. Mandelbrot B. Fraktalna geometrija prirode. – M: Institut za kompjuterska istraživanja, 2002.

5. Morozov A.D. Uvod u teoriju fraktala -Moskva-Iževsk: Institut za kompjuterska istraživanja, 2002, 160 str.

6. Dinamički (algebarski) fraktali // Elementi.. URL:http:// elementy. ru/ posteri/ fraktali/ dinamičan

7. Dinamički (algebarski) fraktali // Elementi.. URL:http:// elementy.ru/posters/fractals/Mandelbrot#nop

8. Algebarski fraktali // Fraktali.. URL:http://rusproject.narod.ru/article/fractals.htm

U poglavljima 6 i 7 predstavili smo Kochove i Peano krive koristeći geomorfologiju da nam pomognu, ali najznačajnije primjene fraktalne teorije su u nešto drugačijim područjima. Polako se približavajući glavnim trendovima u nauci, razmotrićemo u ovom poglavlju (i u naredna dva) dva pitanja izuzetne antike, važnosti i složenosti.

Raspodjela zvijezda, galaksija, jata galaksija i sličnih materija dugo je fascinirala i amatere i stručnjake, ali grupiranje još uvijek ostaje na periferiji astronomije i astrofizike općenito. glavni razlog je da niko nije bio u stanju da objasni zašto se distribucija materije pokorava nepravilnim hijerarhijskim zakonima - barem unutar određenog opsega skala. U mnogim radovima posvećenim ovoj temi može se naći pominjanje fenomena skupljanja, ali se u ozbiljnim teorijskim istraživanjima obično žurno gura pod tepih, tvrdeći da su galaksije raspoređene prilično ujednačeno - na skali koja prelazi neki veliki, ali nedefinisani prag. .

Posmatrajući situaciju iz manje fundamentalne perspektive, možemo reći da nevoljkost da se bavimo neregularnim proizlazi iz nedostatka alata za njegovo matematičko opisivanje. Od statističara se traži da bira između dvije pretpostavke, od kojih se samo jedna može smatrati temeljito ispitanom (asimptotska homogenost). Je li čudo što su rezultati, blago rečeno, neuvjerljivi?

Pitanja su, međutim, takva da ih je teško odbaciti. Mislim da je apsolutno neophodno – uporedo sa nastavkom da pokušavamo da objasnimo grupisanje – pronaći način da se to opiše i čisto modelira stvarnost geometrijske sredine. Pristupajući ovoj temi iz fraktalne perspektive kroz nekoliko poglavlja ovog eseja, nadamo se da ćemo kroz eksplicitne modele pokazati da dokazi sugerišu stepen grupisanja koji daleko prevazilazi granice postavljene za njega postojećim modelima.

Ovo poglavlje treba smatrati uvodnim: ovdje ćemo se upoznati s jednom vrlo utjecajnom teorijom o formiranju zvijezda i galaksija koju je predložio Hoyle, sa osnovnim formalnim modelom njihove distribucije, koji dugujemo Fournieru d'Albuu (ovaj model je također poznat kao Charlierov model), i, što je najvažnije, važno, dobićemo neke empirijske podatke. Pokazaćemo da se i teorija i podaci mogu tumačiti u smislu koncepta fraktalne prašine promjenjive skale. Insistiram da distribucija galaksija i zvijezda uključuje određenu zonu samosličnosti, unutar koje fraktalna dimenzija zadovoljava nejednakost. Osim toga, navode se teorijski razlozi zbog kojih se može očekivati , i, kao posljedica toga, raspravlja se zašto je promatrana vrijednost .

Najava. U poglavlju 22, koristićemo fraktalne alate da poboljšamo naše razumevanje značenja kosmološkog principa, razmotrimo kako se on može i treba modifikovati i naučiti zašto takva modifikacija nužno zahteva slučajnost. Raspravu o klasterima unutar poboljšanog modela odložit ćemo do poglavlja 22, 23 i 32 do 35.

DA LI JE MOGUĆE PRIČATI O GLOBALNOMgustinaSTVAR?

Počnimo tako što ćemo detaljnije pogledati koncept globalne gustine materije. Kao i u slučaju obale, ovdje sve na prvi pogled izgleda vrlo jednostavno, ali u stvarnosti se vrlo brzo - i vrlo zanimljivo - zbuni. Da bi se odredila i izmjerila gustoća, počinje se s masom koncentriranom unutar sfere polumjera sa centrom koji se poklapa sa centrom Zemlje. Ovo procjenjuje približnu gustinu, definiranu kao

Nakon toga vrijednost teži beskonačnosti, a globalna gustoća se definira kao granica do koje konvergira približna gustoća u ovom slučaju.

Međutim, da li se globalna gustoća nužno približava pozitivnoj i konačnoj granici? Ako je tako, onda brzina takve konvergencije ostavlja mnogo da se poželi, i to blago rečeno. Štaviše, procjene maksimalne gustine, kada se razmatraju u vremenskoj perspektivi, ponašaju se prilično čudno. Kako se teleskopska dubina svemira povećavala, približna gustina se smanjivala na iznenađujuće sistematičan način. Prema de Vaucouleursu, uvijek je bilo smanjenja. Uočeni indeks je manji od 3 - u najboljoj aproksimaciji.

De Vaucouleurs je iznio tezu da ponašanje približne vrijednosti gustine odražava stvarnost, što znači da . Ova formula podsjeća na klasični rezultat za kuglu polumjera ugrađenu u euklidski prostor dimenzija - zapreminu takve lopte. U 6. poglavlju naišli smo na istu formulu za Kochovu krivu, s jedinom razlikom što tamo indikator nije bila euklidska dimenzija, već fraktalna dimenzija. A u 8. poglavlju dobili smo formulu za Cantorovo piće na vremenskoj osi (ovdje).

Svi ovi presedani tjeraju (i vrlo uporno) da se pretpostavi da de Vaucouleursov eksponent nije ništa drugo do fraktalna dimenzija.

DA LI SU ZVIJEZDE U OPISU INVARIJANCIJE SKALE?

Očigledno, opseg invarijantnosti skale u kojem je nejednakost zadovoljena ne bi trebalo da uključuje objekte sa eksplicitno definisanim granicama – kao što su planete. Ali da li su zvezde uključene u to? Prema podacima koje je dobio Webbick i predstavljenim u, masa Mliječnog puta unutar sfere radus može se prilično predstaviti u obliku , gdje je vrijednost ekstrapolirana iz galaksija. Mi ćemo, međutim, nastaviti našu raspravu isključivo u galaktičkim terminima.

DA LI OPIS INVARIJANCIJE SKALE IMA GORNJI PRAG?

Pitanje koliko se daleko do vrlo velikih razmjera prostire raspon unutar kojeg se proteže vrlo je kontroverzno, i in U poslednje vreme ponovo je skrenuo pažnju na sebe. Mnogi autori eksplicitno navode ili impliciraju da ovaj raspon dozvoljava postojanje vanjske granice koja odgovara veličini jata galaksija. Drugi autori izražavaju svoje neslaganje sa ovim mišljenjem. De Vaucouleurs tvrdi da je „skupljenje galaksija, a možda i svih drugih oblika materije, dominantna karakteristika strukture Univerzuma na svim vidljivim skalama, bez naznaka bilo kakve aproksimacije homogenosti; prosječna gustina materija se stalno smanjuje kako se uzimaju u obzir veće količine prostora, i nemamo eksperimentalno potvrđenog razloga da vjerujemo da se ovaj trend ne proteže na mnogo veće udaljenosti i manje gustoće.”

Rasprava između ove dvije škole je svakako vrlo zanimljiva i važna – za kosmologiju, ali ne i za naš esej. Čak i ako raspon u kojem , ima granice s obje strane, samo njegovo postojanje je dovoljno značajno da opravda najpažljivije proučavanje.

U svakom slučaju, čini se da Univerzum (baš kao ona klupka konca o kojoj smo govorili u 6. poglavlju) ima više različitih efektivnih dimenzija. Ako počnemo sa skalama reda radijusa Zemlje, tada će prva dimenzija na koju naiđemo biti 3 (ovo je dimenzija čvrste materije sa jasnom granicom). Nadalje, dimenzija pada na 0 (pošto se materija smatra skupom izolovanih tačaka). Slijedi vrlo zanimljiv dio, karakteriziran određenom netrivijalnom dimenzijom koja zadovoljava nejednakost . Ako se grupiranje nepromjenljivo na skali nastavi do beskonačnosti, tada se niz efektivnih dimenzija završava na ovoj posljednjoj vrijednosti. Ako postoji konačan vanjski prag, tada se listi dodaje četvrti interval dimenzija unutar kojeg točke gube svoju individualnost, a mi imamo homogeni plin na rukama, tj. dimenzija se ponovo vraća na 3.

Najnaivnija ideja je da su galaksije približno ravnomjerno raspoređene u Univerzumu. U ovom slučaju, niz dimenzija D se svodi na tri vrijednosti: 3, 0 i opet 3.

< Общая теория относительности утверждает, что при отсутствии материи локальная геометрия пространства стремится стать плоской и евклидовой, в то время как присутствие материи переводит ее в локально риманову. Здесь мы можем говорить о глобально плоской Вселенной, размерность которой равна 3 с локальными значениями . Такой тип возмущений описан в , довольно туманной работе, автор которой приводит (с. 312) пример построения кривой Коха (см. главу 6), не ссылаясь при этом на самого Коха.

FOURNIEROV UNIVERZUM

Sve što treba da uradimo je da konstruišemo fraktal koji zadovoljava pravilo i vidimo kako se slaže sa opšteprihvaćenim pogledima na Univerzum. Prvi detaljni model ove vrste predložio je E. E. Fournier d'Albom (vidi poglavlje 40). Iako je Fournierova knjiga uglavnom fikcija prerušena u naučno istraživanje, ona sadrži nekoliko izuzetno zanimljivih razmatranja o kojima ćemo uskoro razgovarati. Prvo, čini se da Trebali bismo opisati strukturu koju je predložio Fournier.

Započinjemo konstrukciju pravilnim oktaedrom, čija je projekcija prikazana u središtu Sl. 141. Projekcija prikazuje četiri ugla kvadrata, čija dijagonala iznosi 12 "jedinica", i centar ovog kvadrata. Međutim, oktaedar ima još dvije tačke iznad i ispod naše ravni na okomici povučenoj kroz centar kvadrata, na istoj udaljenosti od 6 “jedinica” od ovog centra.

Zatim se svaka tačka zamjenjuje kuglom poluprečnika 1, koju ćemo smatrati "zvezdanim agregatom nultog reda". Najmanja kuglica koja sadrži svih 7 originalnih loptica će se zvati "zvjezdani agregat prvog reda". Agregat drugog reda se dobija povećanjem agregata prvog reda za faktor i zamjenom svake od novih kuglica radijusa 7 kopijom agregata prvog reda. Slično, agregat trećeg reda se dobija povećanjem agregata drugog reda za faktor i zamjenom svake kuglice kopijom agregata drugog reda. I tako dalje.

Ukratko, kada se prelazi između susjednih redova agregacije, i broj bodova i polumjer kuglica se povećavaju za faktor. Prema tome, za bilo koju vrijednost koja je polumjer bilo kojeg agregata, funkcija koja određuje broj točaka sadržanih u kugli polumjera ima oblik . Za srednje, funkcija poprima manje vrijednosti (doseže ), međutim, prema općoj tendenciji, .

Također je moguće interpolirati agregate nultog reda u uzastopnim koracima u agregate reda -1, -2, itd. U prvoj fazi, svaki agregat nultog reda zamjenjujemo kopijom agregata prvog reda, smanjenom za odnos 1/7, i tako dalje. Sa ovom konstrukcijom, relacija ostaje tačna za sve manje vrijednosti. Nakon beskrajne ekstra- i interpolacije, dobijamo sebi sličan skup dimenzija .

Osim toga, dimenzija objekta u 3-prostoru ne obavezuje nužno da to bude prava linija ili bilo koja druga kriva koja se može ispraviti. On čak i ne mora biti koherentan. Svaka dimenzija je kompatibilna sa bilo kojom manjom ili jednakom topološkom dimenzijom. Konkretno, topološka dimenzija Fournierovog univerzuma, beskonačna u oba smjera, jednaka je 0, budući da je potpuno nepovezana "prašina".

DISTRIBUCIJA MASE: FRAKTALNA HOMOGENENOST

Korak od geometrije do distribucije mase čini mi se što je moguće jasnijim. Ako je svaki zvjezdani agregat nultog reda opterećen jediničnom masom, tada je masa unutar lopte poluprečnika identična vrijednosti , i stoga . Štaviše, da bi se od agregata reda nula dobili agregati reda -1, potrebno je razbiti loptu koju smo smatrali homogenom i otkriti da se sastoji od sedam manjih loptica. U ovoj fazi, pravilo važi i za poluprečnike manje od jedinice.

Uzimajući u obzir rezultujuću distribuciju mase po celom 3-prostoru, vidimo da je izuzetno nehomogena, iako na Fournierovom fraktalu nema premca u homogenosti. (Prisjetite se slike 120.) Konkretno, bilo koja dva geometrijski identična dijela Fournierovog univerzuma sadrže iste mase. Predlažem da se ova raspodjela mase nazove fraktalno homogenom.

< Предыдущее определение сформулировано в терминах масштабно-инвариантных фракталов, но концепция фрактальной гомогенности в общем случае гораздо шире. Она применима к любому фракталу, для которого положительна и конечна хаусдорфова мера в размерности . Фрактальная гомогенность требует, чтобы масса, содержащаяся в множестве, была пропорциональна хаусдорфовой мере этого множества.

FOURNIEROV UNIVERZUM JE KAO KANTOROVA PRAŠINA. PROŠIRENJE D0

Nadam se da čitaoca ne zbuni neoprezna upotreba fraktalne terminologije u početnim odeljcima ovog poglavlja. Očigledno je da je Fournier, ne sluteći toga, išao putem koji je bio paralelan putu njegovog savremenog Kantora. Glavna razlika je u tome što je Fournierova konstrukcija ugrađena u prostor, a ne u interval na liniji. Da bi se sličnost dodatno poboljšala, dovoljno je sferne Fournierove agregate zamijeniti blokovima (punjenim kockama). Svaki agregat nultog reda postaje blok čija je dužina stranice 1, a uključuje 7 manjih agregata sa stranom 1/7: središte jednog od njih se poklapa sa centrom originalne kocke, a ostalih šest dodiruju središnji sub -kvadrati na stranama originalne kocke.

U nastavku ćemo pogledati kako je Fournier izveo značenje iz fundamentalnog fizičkog fenomena i kako je Hoyle došao do istog rezultata. Sa geometrijske tačke gledišta, slučaj je poseban, čak i ako se cijelom konstrukcijom pridržavamo oblika i vrijednosti oktaedra. Pošto se kuglice ne preklapaju jedna s drugom, vrijednost može poprimiti bilo koju vrijednost u rasponu od 3 do beskonačnosti, što rezultira zakonom gdje u cijelom intervalu od 0 do .

CHARLIER MODEL I DRUGI FRAKTALNI UNIVERZUM

Gore navedene konstrukcije nisu izbjegle nijedan od nedostataka karakterističnih za prve fraktalne modele. Ono što je najupečatljivije je da je Fournierov model, poput modela Kochove krive u poglavlju 6 i Cantorovog modela prašine u poglavlju 8, groteskno ispravan. Da bi ispravio situaciju, Charlier je predložio pružanje mogućnosti prelaska s jedne hijerarhijske razine na drugu, uzimajući vrijednosti i .

Charlierova reputacija u naučnim krugovima bila je toliko visoka da je, uprkos svim njegovim velikodušnim pohvalama Fournieru, izraženim na svim vodećim jezicima nauke tog vremena, čak i originalni model ubrzo počeo da se pripisuje slavnom tumaču, a ne nikome. . poznati autor. O novom modelu se u to vrijeme naširoko raspravljalo, posebno u . Štaviše, privukla je pažnju veoma uticajnog Emila Borela, čiji su komentari veoma pronicljivi, iako pomalo suvi. Međutim, od tada, osim nekoliko mahnitih pokušaja da se on iznese na vidjelo, Charlierov model je u zaboravu (ne baš uvjerljivi razlozi za takav zaborav su navedeni u str. 20-22 i 408-409). Međutim, ona tvrdoglavo odbija da umre. Glavna ideja je već mnogo puta otkrivena od strane različitih istraživača nezavisno jedni od drugih; posebno preporučujem da je pogledate. (Takođe pogledajte odeljak PAUL LEVY-ja u poglavlju 40.) Ono što smatram najvažnijim je, međutim, da je fraktalna osnova Fournierovog univerzuma implicitna u diskusiji o turbulenciji i galaksijama u radu (vidi Poglavlje 10) iu modelu galaksije genezu, koju je predložio Hoyle (mi ćemo je razmotriti u nastavku).

Glavna fraktalna komponenta je takođe prisutna u mojim modelima (vidi poglavlja 32 do 35).

U tom svjetlu, postavlja se pitanje: da li obrazac distribucije galaksije ne bi bio fraktal sa jednim ili dva praga? Mislim da ne. Ako se složimo da distribucija mora biti nepromjenjiva na skali (razlozi za to su navedeni u Poglavlju 11), i da skup na koji je materija koncentrisana nije standardni skup skale, nemamo izbora nego prihvatiti fraktalnost ovog skupa .

S obzirom na važnost invarijantnosti skale, nije teško razumjeti zašto je Charlierova generalizacija Fournierovog modela bez skale bila osuđena na propast od samog početka.< Оно, кстати, позволяет величине variraju ovisno o tome unutar dvije granice, i . Evo još jedne teme za diskusiju: efektivna dimenzija ne mora imati jednu jedinu vrijednost, ova vrijednost može plivati između gornje i donje granice. Vratit ćemo se na ovu temu u 15. poglavlju.

ZAŠTO JE FOURNIER OČEKIVAOD= 1?

Razgovarajmo sada o vrlo impresivnoj argumentaciji koja je dovela Fourniera do zaključka da bi indikator trebao biti jednak 1 (vidi, str. 103). Ovaj argument sam po sebi je ozbiljan argument u prilog tome da se ne zaboravi ime njegovog autora.

Razmotrimo galaktički agregat proizvoljnog reda s masom i radijusom. Odbacujući besplodne sumnje i primjenjujući na ovaj slučaj formulu za objekte sa sfernom simetrijom, pretpostavimo da je gravitacijski potencijal na površini sfere jednak ( - gravitacijska konstanta). Zvijezda koja pada na naš svemir sudara se s njegovom površinom velikom brzinom .

Prema Fournieru, vrlo važan zaključak može se izvući iz činjenice da se nijedna uočljiva zvijezda ne kreće brzinom većom od 1/300 brzine svjetlosti. Masa sadržana u svjetskoj kugli raste direktno proporcionalno njenom polumjeru, a ne zapremini, ili, drugim riječima, gustina materije unutar svjetske lopte obrnuto je proporcionalna njenoj površini... Objasnimo posljednje izjava - potencijal na površini sfere je uvijek isti, jer je direktno proporcionalan masi materije unutar sfere i obrnuto proporcionalan udaljenosti od centra. Kao posljedica toga, brzine zvijezda bliske brzini svjetlosti nisu uobičajene ni u jednom dijelu Univerzuma.

REZANJE NA HOYLE; JEANS KRITERIJ

Hijerarhijska distribucija se pojavljuje i u Hoyleovoj teoriji (vidi), prema kojoj se galaksije i zvijezde formiraju kroz kaskadni proces, a ovaj proces počinje homogenim plinom.

Razmotrimo oblak gasa mase, zagrijan na temperaturu i raspoređen ujednačene gustine unutar lopte poluprečnika. Kao što je Gine pokazala, kada dolazi do “kritične” situacije. (Ovde je Boltzmanova konstanta, a je numerički koeficijent.) Budući da je u kritičnom stanju, primarni oblak gasa je nestabilan i mora se neizbežno smanjiti.

Hoyle postulira da (a) veličina dosegne kritičnu vrijednost negdje na samom početku, (b) kompresija prestaje kada se zapremina oblaka gasa smanji na 1/25 njegove prvobitne zapremine, i (c) svaki oblak u ovoj fazi razbija na pet manjih oblaka sa iste veličine, mase i poluprečnika. Odnosno, proces se vraća na isto mjesto gdje je započeo: njegov rezultat je nestabilno stanje, nakon čega slijedi druga faza kompresije i razdvajanja, zatim treća, itd. Urušavanje prestaje tek kada oblaci postanu toliko neprozirni da se zadržavaju. rezultujući Kada se gas komprimuje, unutra je toplota.

Kao iu raznim drugim oblastima u kojima se javljaju slični kaskadni procesi, predlažem da se na ovaj slučaj primeni opšta terminologija, odnosno pet oblaka ćemo nazvati curds, a sam kaskadni proces - podsirenje. Kao što sam spomenuo prilikom predstavljanja posljednjeg pojma, jednostavno nisam mogao odoljeti aluzijama na galaksije.

Radi pogodnosti u grafičkom predstavljanju svog modela, Fournier uvodi , dok Hoyle tvrdi da je vrijednost fizički opravdana. Detalji Fournierove geometrijske ilustracije nadilaze bilo koje razumne ili neophodne granice. Hoyleove izjave o prostornoj strukturi svježeg sira, naprotiv, prilično su nejasne. Za detaljnu implementaciju Hoyleovog modela moraćemo da sačekamo do 23. poglavlja, gde posmatramo nasumično preklapanje. Kako god bilo, pomenuta odstupanja nisu od suštinske važnosti: glavna stvar je da, odnosno indikator mora postati sastavni dio naše konstrukcije ako želimo da se sirenje završi u istom stanju iz kojeg je i počelo. , - i naime, nestabilnost Jeansa.

Osim toga, ako se trajanje prve faze uzme kao 1, tada će, prema podacima plinske dinamike, trajanje te faze biti . Posljedično, ukupno trajanje cijelog procesa, koji se sastoji od beskonačnog broja faza, ne prelazi 1.2500.

EKVIVALENTNOST FOURNIEROVA I HOYLEOVA PRISTUPA ZAKLJUČKUD= 1

Na granici nestabilnog oblaka gasa koji zadovoljava Jeansov kriterijum, brzina i temperatura su povezane relacijom , budući da su jednake i (Fournier) i (Gene). Sjetimo se sada da je u statističkoj termodinamici temperatura plina direktno proporcionalna srednjoj kvadratnoj brzini njegovih molekula. To znači, iz kombinacije Fournierovih i Jeansovih kriterija, možemo pretpostaviti da je na granici oblaka brzina pada makroskopskog objekta direktno proporcionalna prosječna brzina njegovih molekula. Pažljiva analiza uloge temperature u Jeansovom kriteriju sigurno će pokazati da su ova dva kriterija ekvivalentna.< Вероятнее всего, аналогия распространяется и на справедливость отношения внутри галактик, о чем сообщает Валленквист в .

ZAŠTOD= 1,23, A NED= 1?

Nesklad između empirijskog i teorijskog značenja Fourniera i Hoylea podiže važan problem. P. J. E. Peebles ju je ispitao 1974. iz perspektive teorije relativnosti. U njegovom radu fizički i statistički (ali ne i geometrijski) aspekti pomenutog problema dobili su iscrpno pokriće.

FRAKTALNA DIMENZIJA NEBA

Nebo je projekcija Univerzuma. Da bi se dobila ova projekcija, svaka tačka Univerzuma se prvo opisuje sfernim koordinatama , i , a zatim se koordinata zamjenjuje sa 1. Ako je Univerzum fraktal s dimenzijom , i porijeklo referentnog sistema pripada upravo ovom Univerzumu ( vidi poglavlje 22), tada je struktura projekcije, po pravilu, definisana sljedećom alternativom: podrazumijeva da projekcija pokriva neko područje neba različito od nule, dok znači da sama projekcija ima fraktalnu dimenziju .< Как показано на рис. 141 и 143, «правило» не лишено исключений, обусловленных структурой фрактала и/или/ выбором точки отсчета. О таких правилах часто говорят «истинно с вероятностью 1».

NAPOMENA O EFEKTU GORENOG NEBA (POGREŠNO ZVAN OLBERSOV PARADOKS)

Pravilo iz prethodnog odjeljka ima mnogo veze s motivacijom koja je navela različite istraživače (uključujući Fourniera) da otkriju vlastite verzije fraktalnog univerzuma. Shvatili su da takvi univerzumi geometrijski "poništavaju" efekat gorućeg neba, koji se takođe često (ali netačno) naziva Olbersovim paradoksom. Ako pretpostavimo da je distribucija nebeskih tijela ujednačena (odnosno na svim skalama), onda bi nebo iznad nas trebalo biti gotovo ravnomjerno osvijetljeno i noću i danju, a svjetlina ovog osvjetljenja bi trebala biti uporediva sa suncem .

Ovaj paradoks više ne zanima fizičare, budući da je poništen teorijom relativnosti, teorijom svemira koji se širi i drugim razmatranjima. Međutim, njegova smrt je imala zanimljivu nuspojavu: brojni komentatori počeli su citirati svoja omiljena objašnjenja za efekat užarenog neba - neki u nadi da će opravdati svoj prezir prema grupisanju, dok drugi, naprotiv, potpuno poriču njegovu stvarnost. Vrlo čudno gledište, moram reći. Čak i ako pretpostavimo da grupisanje galaksija nema nikakve veze s odsustvom efekta gorućeg neba, ono i dalje postoji - i zahtijeva odgovarajuće proučavanje. Štaviše, kao što ćemo videti u 32. poglavlju, koncept univerzuma koji se širi je kompatibilan ne samo sa standardnom homogenošću, već i sa fraktalnom homogenošću.

Efekat blještavog neba objašnjava se vrlo jednostavno. Budući da je količina svjetlosti koju emituje zvijezda direktno proporcionalna njenoj površini, količina svjetlosti koja dopire do posmatrača koji se nalazi na udaljenosti od zvijezde mora biti , ali i vidljiva površina zvijezde mora biti . Dakle, omjer količine svjetlosti i prividnog sfernog kuta ne ovisi o . Osim toga, ako je distribucija zvijezda u Univerzumu ujednačena, tada će gotovo bilo koji smjer u kojem pogledate prije ili kasnije naići na neku zvijezdu. Posljedično, nebo je ravnomjerno obasjano svjetlošću zvijezda i čini se blistavim. (Mjesečev disk u ovom slučaju formira isključivo tamno područje - barem u odsustvu atmosferske difuzije.)

Ako pretpostavimo da je Univerzum fraktalan i da je njegova dimenzija , tada se paradoks rješava sam od sebe. U ovom slučaju, projekcija Univerzuma na nebeski svod je fraktalni skup iste dimenzije, odnosno skup nulte površine. Čak i ako zvijezde imaju radijus različit od nule, većina smjerova ide u beskonačnost bez susreta sa niti jednom zvijezdom na svom putu. Ako pogledamo ovim pravcima, videćemo samo crnilo noćnog neba. Ako nakon intervala u kojem , slijedi interval u kojem , tada pozadina neba neće biti strogo crna, već izuzetno slabo osvijetljena.

Kepler je skrenuo pažnju na efekat gorućeg neba nedugo nakon što je Galileo, u svojoj „Zvezdanoj poruci“, pozitivno govorio o ideji neograničenog Univerzuma. U svom “Razgovoru sa zvjezdanim glasnikom” (1610), Kepler je iznio sljedeći prigovor: “Uopšte se ne ustručavate da izjavite da je vidljivo više od 10.000 zvijezda... Ako je to tako, i ako [zvijezde ] su iste prirode kao i naše Sunce, zašto onda sva ova sunca zajedno ne premašuju naše Sunce po sjaju?... Možda su pomračena eterom? Ni u najmanjem stepenu... Apsolutno je očigledno da naš svijet ni na koji način ne može pripadati neurednom roju bezbroj drugih svjetova” (vidi, str. 34-35).

Zaključak je bio prilično kontroverzan, ali argumentacija nije zaboravljena – dokaz za to je primjedba Edmunda Halleya (koju je iznio 1720.): „Čuo sam za još jedan prigovor, koji kaže da ako je broj fiksnih zvijezda veći od konačni, onda bi cijeli luk njihove vidljive sfere bio potpuno osvijetljen.” O ovom prigovoru su kasnije raspravljali de Chezo i I. G. Lambert, ali je njegovo autorstvo pripisano veliki prijatelj Gauss njemačkom astronomu Olbersu. Termin "Olbersov paradoks", koji se od tada koristi za opisivanje ove kontradikcije, skandalozan je, ali simptomatičan. Rezultati zapažanja koji spadaju u kategoriju „ne podliježu klasifikaciji“ (vidi str. 51) često se pripisuju prvom predstavniku zvanične većine, koji će ih ukrasiti omotom koji se može u potpunosti klasificirati, makar i samo privremenim. Rasprava o ovoj temi u istorijskoj perspektivi može se naći u.

NAPOMENA O NJUTONOVOJ GRAVITACIJI

Velečasni Bentley je stalno gnjavio Newtona jednim zapažanjem koje je blisko povezano s efektom gorućeg neba: ako je distribucija zvijezda ujednačena, onda je sila kojom one djeluju jedna na drugu beskonačna. Možemo dodati da je i njihov gravitacioni potencijal beskonačan. I da će svaka distribucija u kojoj , dati općenito beskonačan potencijal u svim slučajevima osim . Moderna teorija potencijala (Frostmanova teorija) potvrđuje činjenicu da postoji neka posebna veza između Newtonove gravitacije i vrijednosti. Pokazatelj koji su dobili Fournier i Hoyle također treba pripisati manifestacijama ove veze.< Положение Фурнье о том, что «гравитационный потенциал на поверхности сферы всегда одинаков», является центральным в moderna teorija potencijal. " Kvadrat omjera brzina koji postulira Fournier nalazi se tačno u sredini navedenog intervala.

AGLUTINIRANI FRAKTALNI UNIVERZUM?

Mnogi istraživači vjeruju da se formiranje zvijezda i drugih nebeskih objekata može objasniti uzlaznom kaskadom (tj. postepenom aglutinacijom visoko raspršenih čestica prašine u sve veće komade), a da ne žele ništa čuti o silaznoj kaskadi a 1a Hoyle (tj. , postepena fragmentacija veoma velikih i raspršenih masa na sve manje delove).

Slična alternativa se javlja u vezi sa kaskadama postuliranim u teoriji turbulencije (vidi Poglavlje 10). Ričardsonova kaskada ide prema dole ka sve manjim vrtlozima, ali kaskade prema gore takođe mogu da učestvuju u procesu (vidi Poglavlje 40, odeljak LEWIS FRY RICHARDSON). Stoga se nadamo da će odnos između silazne i uzlazne kaskade uskoro biti pravilno objašnjen.

FRAKTALNI NIZOVI TELESKOPA

Teško da može postojati prikladniji završni pečat ove rasprave od napomene u vezi s instrumentima pomoću kojih se galaksije posmatraju. Da bi se poboljšao kvalitet posmatranja, Dyson predlaže zamjenu velikih pojedinačnih teleskopa nizovima malih teleskopa. Promjer svakog od malih teleskopa trebao bi biti oko 0,1 m (veličina najmanjeg optički značajnog atmosferskog poremećaja), njihovi centri bi trebali činiti fraktalni hijerarhijski obrazac, a vezu između teleskopa osiguravat će Curry interferometri. Gruba analiza dovodi do zaključka da kao odgovarajuću vrijednost dimenzije treba uzeti 2/3. Evo Dysonovog vlastitog zaključka: „Niz od tri kilometra od 1024 teleskopa od deset centimetara međusobno povezanih sa 1023 interferometra nije najpraktičniji prijedlog danas. [Izneo sam to] kao teorijsku ideju da pokaže šta bi, u principu, moglo da se uradi ovde.”

PREGLED NASLUČAJNIH FRAKTALNIH MODELA GALAKSIJA

Ako vjerujemo da je moguće učinkovito opisati distribuciju galaksija korištenjem nasumično otkrivenih fraktalnih modela koji nisu ni kompleksni ni univerzalni, ne bi trebalo biti iznenađujuće da nam namjerno fraktalni slučajni modeli mogu pružiti mnogo više efektivni opisi. Za početak, možemo mnogo bolje razumjeti Hoyleovo savijanje ako ga posmatramo u njegovom odgovarajućem okruženju, odnosno među slučajnim fraktalima (vidi Poglavlje 23). Od još većeg značaja, po mom mišljenju, su nasumični modeli koje sam razvio, a o kojima ćemo govoriti u poglavljima 32 do 35. Jedan od argumenata u prilog razmatranja više modela je da poboljšanje kvaliteta opisa dolazi po cenu povećanja složenost. Drugi argument je da je svaki model izgrađen na posebnoj fraktalnoj prašini, od kojih svaki zaslužuje posebno razmatranje. Razmotrimo ukratko ove modele po logičkom redu.

Oko 1965. krenuo sam da pružim odnos sa odgovarajućim modelom u kojem bi „centar univerzuma“ bio odsutan kao koncept. Prvo sam postigao ovaj cilj koristeći model slučajnog hoda opisanog u poglavlju 32. Zatim sam, kao alternativu, razvio model trem, čija je suština bila da je izrezan određeni skup međusobno nezavisnih i nasumično postavljenih tremova slučajnog polumjera. prostora, a gornja granica radijusa mogla bi doseći gornji prag, koji može biti konačan ili beskonačan.

Budući da su oba modela odabrana isključivo iz razloga formalne jednostavnosti, bio sam ugodno iznenađen njihovom prediktivnom vrijednošću. Pokazalo se da se moje teorijske korelacijske funkcije dobro slažu sa funkcijama prilagođenim krivuljama koje je dao Peebles (vidi, str. 243-249).< Точнее, два моих приближения совпали на двухточечной корреляции, случайные блуждания дали хорошую трех- и плохую четырехточечную корреляции, а сферические тремы оказались на высоте во всех известных корреляциях.

Nažalost, primjeri generirani ovim modelima izgledaju potpuno nerealno. Koristeći koncept koji sam razvio posebno za ovu svrhu, o kojem ću raspravljati u 35. poglavlju, moji rani modeli pokazuju neprihvatljiva svojstva lakuna. U slučaju trem modela, ovaj nedostatak se može ispraviti uvođenjem složenijih trem oblika. Za model slučajnog hoda, koristio sam manje lakunarni „podređeni“.

Stoga je proučavanje klastera galaksija značajno podstaklo razvoj fraktalne geometrije. Trenutno se opseg primjene fraktalne geometrije u proučavanju klastera galaksija značajno proširio, nadilazeći one generalno čišćenje i otklanjanje grešaka koje smo preduzeli u ovom poglavlju.

BEZ DIJAMANTA KAO ZVIJEZDE

Raspodjela naslaga dijamanata u zemljinoj kori vrlo je slična raspodjeli zvijezda i galaksija na nebeskom svodu. Zamislite veliku mapu svijeta, na kojoj je svaki rudnik dijamanata, svako bogato ležište - koje se sada razvija ili je već napušteno - označeno iglom. Ako kartu pogledamo sa dovoljno velike udaljenosti, vidjet ćemo da je distribucija iglica krajnje neravnomjerna. Postoji nekoliko izoliranih pribadača razbacanih tu i tamo, ali većina je koncentrirana u nekoliko blagoslovljenih (ili prokletih) područja. Površina zemlje unutar ovih područja, zauzvrat, uopće nije ravnomjerno popločana dijamantima. Ako pažljivije pogledamo svaku od njih, opet vidimo da većina područja ostaje prazna, dok nekoliko raštrkanih podoblasti pokazuje značajno povećanu koncentraciju dijamanata. Ovaj proces se može nastaviti kroz nekoliko redova veličine.

Jeste li u iskušenju da u ovom kontekstu primijenite koncept sirenja? Sa svoje strane, reći ću da takav model postoji, predložio ga je de Wis, a mi ćemo ga razmotriti u poglavlju 39 u odeljku NELAKUNARNI FRAKTALI.

Fournierova knjiga nudi sljedeće objašnjenje za ovu ilustraciju: „Multiverzum, izgrađen na principu križa ili oktaedra, nije plan našeg svijeta, već pomaže da se pokaže mogućnost postojanja beskonačnog broja sličnih uzastopnih svemira. bez izazivanja efekta "zapaljenog neba". Količina materije u svakoj svjetskoj sferi direktno je proporcionalna njenom radijusu. Ovaj uslov je neophodan da bi se ispunili zakoni gravitacije i zračenja. U nekim pravcima nebo izgleda potpuno crno - uprkos činjenici da je broj univerzuma beskonačan. "Svjetski broj" u u ovom slučaju nije kao u stvarnom svijetu." umjesto . Izgradnja se nastavlja korak dalje nego što je to moguće na Sl. 141.

(Dinamički) fraktali

Fraktali ovog tipa nastaju prilikom proučavanja nelinearnih dinamičkih sistema (otuda i naziv). Ponašanje takvog sistema može se opisati kompleksnom nelinearnom funkcijom (polinomom) f(z). Uzmimo neku početnu tačku z0 na kompleksnoj ravni. Sada razmotrimo beskonačan niz brojeva na kompleksnoj ravni, od kojih je svaki dobijen iz prethodnog: z0, z1 = f(z0), z2 = f(z1), ... zn+1 = f(zn). U zavisnosti od početne tačke z0, takav niz se može ponašati različito: teži ka beskonačnosti kao n → ∞; konvergirati do neke krajnje tačke; ciklički uzimati niz fiksnih vrijednosti; Moguće su i složenije opcije.

Dakle, bilo koja tačka z kompleksne ravni ima svoje ponašanje tokom iteracija funkcije f(z), a cijela ravan je podijeljena na dijelove. Štoviše, točke koje leže na granicama ovih dijelova imaju sljedeće svojstvo: s proizvoljno malim pomakom, priroda njihovog ponašanja se naglo mijenja (takve se točke nazivaju točke bifurkacije). Dakle, ispada da skupovi tačaka koji imaju jednu specifičnu vrstu ponašanja, kao i skupovi tačaka bifurkacije, često imaju fraktalna svojstva. Ovo su Julia skupovi za funkciju f(z).

Mandelbrotov skup je konstruisan nešto drugačije. Razmotrimo funkciju fc(z) = z2 + c, gdje je c kompleksan broj. Konstruirajmo niz ove funkcije sa z0 = 0; ovisno o parametru c, može divergirati do beskonačnosti ili ostati ograničen. Štaviše, sve vrijednosti c za koje je ovaj niz ograničen čine Mandelbrotov skup. Detaljno su ga proučavali sam Mandelbrot i drugi matematičari, koji su otkrili mnoga zanimljiva svojstva ovog skupa.

Može se vidjeti da su definicije skupova Julia i Mandelbrot slične jedna drugoj. Zapravo, ova dva skupa su usko povezana. Naime, Mandelbrotov skup su sve vrijednosti kompleksnog parametra c za koje je povezan Julijev skup fc(z) (skup se naziva povezanim ako se ne može podijeliti na dva disjunktna dijela, uz neke dodatne uvjete).

Ovo je najveća grupa fraktala. Dobivaju se korištenjem nelinearnih procesa u n-dimenzionalnim prostorima. Dvodimenzionalni procesi su najviše proučavani. Kada se nelinearni iterativni proces tumači kao diskretni dinamički sistem, može se koristiti terminologija teorije ovih sistema: fazni portret, stabilni proces, atraktor itd.

Poznato je da nelinearni dinamički sistemi imaju nekoliko stabilnih stanja. Stanje u kojem se dinamički sistem nalazi nakon određenog broja iteracija zavisi od njegovog početnog stanja. Dakle, svako stabilno stanje (ili, kako se kaže, atraktor) ima određeno područje početnih stanja, iz kojih će sistem nužno pasti u konačna stanja koja se razmatraju. Tako je fazni prostor sistema podijeljen na područja privlačenja atraktora. Ako je fazni prostor dvodimenzionalan, tada se boje područja privlačnosti različite boje, možete dobiti fazni portret u boji ovog sistema (iterativni proces). Promjenom algoritma za odabir boja, možete dobiti složene fraktalne uzorke s bizarnim višebojnim uzorcima. Iznenađenje za matematičare bila je sposobnost generiranja vrlo složenih netrivijalnih struktura korištenjem primitivnih algoritama.

Kao primjer, razmotrite Mandelbrotov skup (vidi slike 3 i 4). Algoritam za njegovu konstrukciju je prilično jednostavan i baziran je na jednostavnom iterativnom izrazu:

Z = Z[i] * Z[i] + C,

gdje su Zi i C kompleksne varijable. Iteracije se izvode za svaku početnu tačku C pravokutnog ili kvadratnog područja - podskupa kompleksne ravni. Iterativni proces se nastavlja sve dok Z[i] ne pređe krug radijusa 2, čije središte leži u tački (0,0), (to znači da je atraktor dinamičkog sistema beskonačan), ili nakon dovoljnog veliki broj iteracija (na primjer 200-500) Z[i] će konvergirati u neku tačku na krugu. U zavisnosti od broja iteracija tokom kojih je Z[i] ostao unutar kruga, možete podesiti boju tačke C (ako Z[i] ostane unutar kruga dovoljno veliki broj iteracija, proces iteracije se zaustavlja i ovaj raster tačka je obojena crnom bojom).

Gornji algoritam daje aproksimaciju takozvanom Mandelbrotovom skupu. Mandelbrotov skup sadrži tačke koje ne idu u beskonačnost tokom beskonačnog broja iteracija (tačke koje su crne). Tačke koje pripadaju granici skupa (tu nastaju složene strukture) idu u beskonačnost u konačnom broju iteracija, a tačke koje leže izvan skupa idu u beskonačnost nakon nekoliko iteracija (bijela pozadina).

Primjeri algebarskih fraktala:

Mandelbrot set
Julia postavlja
Halejev fraktal
Njutnov fraktal

- 213,50 Kb

MINISTARSTVO OBRAZOVANJA, NAUKE, OMLADINE I SPORTA UKRAJINE

ODESSKA DRŽAVNA AKADEMIJA GRAĐEVINARSTVA I ARHITEKTURE

ODSJEK ZA FIZIKU

SAŽETAK

Disciplina: “Nauka o fizičkim materijalima”

Na temu: "FRAKTALI"

Završeno:

st. gr. ZPGS – 501 M

Zlunyaev E.A.

s/kn br. 08070

Provjereno:

prof., Gerega A.N.

Odesa - 2013

FRAKTALI

Uvod

1. Šta su fraktali

2. Klasični fraktali

2.1 Kochova pahulja

2.2 Ubrus i tepih Sierpinskog

3. L-sistemi

4. Praktična primjena fraktala

Književnost

Uvod

Kada se većini ljudi činilo da je geometrija u prirodi ograničena na tako jednostavne figure kao što su linija, krug, konusni presjek, poligon, sfera, kvadratna površina, kao i njihove kombinacije. Na primjer, šta može biti ljepše od izjave da su planete u našoj Solarni sistem kretati se oko Sunca po eliptičnim orbitama?

Međutim, mnogi prirodni sistemi su toliko složeni i nepravilni da korištenje samo poznatih objekata klasične geometrije za njihovo modeliranje izgleda beznadežno. Kako, na primjer, možete napraviti model planinskog lanca ili krošnje drveta u smislu geometrije? Kako opisati raznolikost bioloških konfiguracija koje opažamo u svijetu biljaka i životinja? Zamislite kompleksnost krvožilnog sistema, koji se sastoji od mnogih kapilara i sudova koji isporučuje krv u svaku ćeliju ljudskog tijela. Zamislite kako su pametno raspoređena pluća i pupoljci, koji po strukturi podsjećaju na drveće s razgranatom krošnjom.

Dinamika stvarnih prirodnih sistema može biti jednako složena i nepravilna. Kako pristupiti modeliranju kaskadnih vodopada ili turbulentnih procesa koji određuju vrijeme?

Fraktali i matematički haos su pogodni alati za istraživanje ovih pitanja. Termin fraktal odnosi se na neku statičnu geometrijsku konfiguraciju, kao što je snimak vodopada. Haos je dinamički termin koji se koristi za opisivanje fenomena sličnih turbulentnom vremenu. Često nas ono što opažamo u prirodi zaintrigira beskonačnim ponavljanjem istog obrasca, uvećanim ili smanjenim koliko god puta želimo. Na primjer, drvo ima grane. Na ovim granama se nalaze manje grane itd. Teoretski, element grananja se ponavlja beskonačno, postajući sve manji i manji. Ista stvar se može vidjeti kada se pogleda fotografija planinskog terena. Pokušajte malo zumirati planinski lanac - opet ćete vidjeti planine. Tako se manifestuje svojstvo samosličnosti karakteristično za fraktale.

Veliki dio rada na fraktalima koristi samosličnost kao svojstvo definiranja. Slijedeći Benoita Madelbrota, prihvatamo gledište da fraktale treba definirati u terminima fraktalne (frakcionalne) dimenzije. Odatle potiče i riječ fraktal (od latinskog fractus - razlomak).

Koncept frakcijske dimenzije je složen koncept koji se prikazuje u nekoliko faza. Prava linija je jednodimenzionalni objekat, dok je ravan dvodimenzionalni objekat. Ako ravnu liniju i ravninu dobro uvrnete, možete povećati dimenziju rezultirajuće konfiguracije; u ovom slučaju, nova dimenzija će obično biti u nekom smislu frakcijska, što moramo razjasniti. Veza između frakcijske dimenzije i samosličnosti je u tome što je uz pomoć samosličnosti moguće na najjednostavniji način konstruirati skup razlomne dimenzije. Čak iu slučaju mnogo složenijih fraktala, kao što je granica Mandelbrotovog skupa, gdje ne postoji čista samosličnost, dolazi do gotovo potpunog ponavljanja osnovnog oblika u sve smanjenom obliku.

Šta su fraktali

Fraktali su poznati skoro jedan vek, dobro su proučavani i imaju brojne primene u životu. Ovaj fenomen je zasnovan na veoma jednostavna ideja: beskrajna raznolikost oblika u ljepoti i raznolikosti može se dobiti iz relativno jednostavnih dizajna koristeći samo dvije operacije - kopiranje i skaliranje.

Ovaj koncept nema strogu definiciju. Dakle, riječ "fraktal" nije matematički pojam. Ovo je obično ime koje se daje geometrijskoj figuri koja zadovoljava jedno ili više od sljedećih svojstava: ima složenu strukturu pri bilo kojem povećanju; je (približno) sebi sličan; ima frakcijsku Hausdorffovu (fraktalnu) dimenziju, koja je veća od topološke; mogu se konstruisati rekurzivnim procedurama.

Na prelazu iz 19. u 20. vek proučavanje fraktala bilo je više epizodično nego sistematično, jer su matematičari ranije uglavnom proučavali „dobre“ objekte koji su se mogli proučavati korišćenjem opštih metoda i teorija. Godine 1872. njemački matematičar Karl Weierstrass konstruirao je primjer kontinuirane funkcije koja se nigdje ne može razlikovati. Međutim, njegova konstrukcija je bila potpuno apstraktna i teško razumljiva. Stoga je 1904. Šveđanin Helge von Koch osmislio kontinuiranu krivu koja nigdje nema tangente i koju je prilično lako nacrtati. Ispostavilo se da ima svojstva fraktala. Jedna varijanta ove krive se zove “Koch pahulja”.

Ideje o samosličnosti figura preuzeo je Francuz Paul Pierre Levy, budući mentor Benoita Mandelbrota. Godine 1938. objavljen je njegov članak "Ravne i prostorne krive i površine koje se sastoje od dijelova sličnih cjelini", u kojem je opisan još jedan fraktal - Levyjeva C-kriva. Svi ovi gore navedeni fraktali mogu se uslovno svrstati u jednu klasu konstruktivnih (geometrijskih) fraktala. Druga klasa su dinamički (algebarski) fraktali, koji uključuju Mandelbrotov skup. Prva istraživanja u ovom pravcu datiraju s početka 20. stoljeća i vezuju se za imena francuskih matematičara Gastona Julije i Pierre Fatoua. Julia je 1918. godine objavila rad od skoro dvije stotine stranica o iteracijama složenih racionalnih funkcija, koji opisuje Julijine skupove – cijelu porodicu fraktala blisko povezanih s Mandelbrotovim skupom. Ovaj rad je dobio nagradu Francuske akademije, ali nije sadržavao niti jednu ilustraciju, tako da je bilo nemoguće cijeniti ljepotu otvorenih objekata. Uprkos činjenici da je ovo djelo učinilo Juliju poznatom među matematičarima tog vremena, brzo je zaboravljeno.

Ponovo se pažnja na rad Julije i Fatoua okrenula tek pola veka kasnije, sa pojavom kompjutera: upravo su oni učinili vidljivim bogatstvo i lepotu sveta fraktala. Na kraju krajeva, Fatou nikada nije mogao pogledati slike koje danas poznajemo kao slike Mandelbrotovog skupa, jer se potreban broj proračuna ne može izvršiti ručno. Prva osoba koja je koristila kompjuter za ovo bio je Benoit Mandelbrot.

Godine 1982. objavljena je Mandelbrotova knjiga “Fraktalna geometrija prirode” u kojoj je autor prikupio i sistematizovao gotovo sve informacije o fraktalima koje su tada bile dostupne i prikazao ih na jednostavan i pristupačan način. Mandelbrot je glavni naglasak u svom izlaganju stavio ne na teške formule i matematičke konstrukcije, već na geometrijsku intuiciju čitatelja. Zahvaljujući kompjuterskim ilustracijama i povijesnim pričama, kojima je autor vješto razvodnio naučnu komponentu monografije, knjiga je postala bestseler, a fraktali poznati široj javnosti. Njihov uspjeh među nematematičarima uvelike je posljedica činjenice da su uz pomoć vrlo jednostavni dizajni i formule koje čak i srednjoškolac može da razume, dobijene slike su neverovatne po složenosti i lepoti. Kada su personalni računari postali dovoljno moćni, pojavio se čak i čitav pravac u umetnosti - fraktalno slikanje, a to je mogao da uradi skoro svaki vlasnik računara. Sada na Internetu možete lako pronaći mnoge stranice posvećene ovoj temi.

1.1. Geometrijski (konstruktivni) fraktali

Fraktali ovog tipa se grade u fazama. Prvo je prikazana baza. Zatim se neki dijelovi baze zamjenjuju fragmentom. U svakoj sljedećoj fazi, dijelovi već izgrađene figure, slični zamijenjenim dijelovima baze, ponovo se zamjenjuju fragmentom uzetim u odgovarajućoj mjeri. Svaki put se skala smanjuje. Kada promjene postanu vizualno neprimjetne, vjeruje se da konstruirana figura približava fraktalni bunar i daje predstavu o njegovom obliku. Da bi se dobio sam fraktal, potreban je beskonačan broj faza. Promjenom baze i fragmenta možete dobiti mnogo različitih geometrijskih fraktala.

Geometrijski fraktali su dobri jer su, s jedne strane, predmet prilično ozbiljnog naučnog proučavanja, a s druge strane, mogu se "vidjeti" - čak i osoba daleko od matematike u njima će pronaći nešto za sebe. Ova kombinacija je rijetka u modernoj matematici, gdje su svi objekti definirani korištenjem nejasnih riječi i simbola. Ispostavilo se da se mnogi geometrijski fraktali mogu nacrtati doslovno na komadu kockastog papira. Odmah napravimo rezervu da su sve rezultirajuće slike (uključujući i one prikazane na ovom posteru) samo konačne aproksimacije suštinski beskonačnih fraktala. Ali uvijek možete nacrtati takvu aproksimaciju da oko neće razlikovati vrlo male detalje i naša mašta će moći stvoriti ispravnu sliku fraktala. Na primjer, s obzirom na dovoljno veliki list milimetarskog papira i malo slobodnog vremena, možete ručno nacrtati tako preciznu aproksimaciju tepiha Sierpinski da će ga s udaljenosti od nekoliko metara golim okom percipirati kao pravi fraktal. Računar će uštedjeti vrijeme i papir i istovremeno povećati tačnost crtanja.

Snowflake Koch

T-kvadrat; H-fraktal

Sierpinski trougao

Pitagorino drvo

Levy kriva

1.2. Dinamički (algebarski) fraktali

Mandelbrot set

Julia postavlja

Halejev fraktal

Njutnov fraktal

2. Klasični fraktali

2.1 Kochova pahulja

Početkom dvadesetog veka matematičari su tražili krivulje koje ni u jednoj tački nemaju tangentu. To je značilo da je kriva naglo promijenila smjer, i to enormno velikom brzinom (izvod je bio jednak beskonačnosti). Potraga za ovim krivuljama nije bila uzrokovana samo praznim zanimanjem matematičara. Činjenica je da se početkom dvadesetog veka kvantna mehanika razvijala veoma brzo. Istraživač M. Brown je skicirao putanju kretanja suspendiranih čestica u vodi i objasnio ovaj fenomen na sljedeći način: nasumično pokretni atomi tekućine udaraju u suspendirane čestice i time ih pokreću. Nakon ovog objašnjenja Brownovog kretanja, naučnici su se suočili sa zadatkom pronalaženja krive koja bi najbolje aproksimirala kretanje Brownovih čestica. Da bi se to postiglo, kriva je morala zadovoljiti sljedeća svojstva: da nema tangente ni u jednoj tački. Matematičar Koch je predložio jednu takvu krivu. Nećemo ulaziti u objašnjenja pravila za njegovu konstrukciju, već ćemo jednostavno prikazati njenu sliku iz koje će sve postati jasno (slika 1.1.1).

Slika 2.1.1. Snowflake Koch.

Jedan važna imovina, koju ima granica Kochove pahulje - njena beskonačna dužina. Ovo može izgledati iznenađujuće jer smo navikli da se bavimo krivuljama koje nisu u toku matematička analiza. Obično glatke ili barem po komadima glatke krive uvijek imaju konačnu dužinu (što se može provjeriti integracijom). Mandelbrot je, s tim u vezi, objavio niz fascinantnih radova koji istražuju pitanje mjerenja dužine obale Velike Britanije. Kao model on

Rice. 2.1.2. Konstrukcija Kochove pahulje.

koristio je fraktalnu krivulju, koja podsjeća na ivicu pahulje, osim što je uvela element slučajnosti kako bi se uzela u obzir slučajnost u prirodi. Kao rezultat toga, pokazalo se da kriva koja opisuje obalu ima beskonačnu dužinu.

2.2 Ubrus i tepih Sierpinskog

Još jedan primjer jednostavnog samosličnog fraktala je ubrus Sierpinski (slika 1.2.1), koji je izumio poljski matematičar Waclaw Sierpinski 1915. godine. Sam pojam salveta pripada Mandelbrotu. U metodi izgradnje ispod, počinjemo sa određenim regionom i sekvencijalno eliminišemo unutrašnje podregije. Kasnije ćemo razmotriti druge metode, posebno korištenje L-sistema, kao i bazirane na iteriranim funkcijama.

Slika 2.2.1. Sierpinski salveta

Neka je početni skup S0 jednakostranični trougao zajedno sa područjem koje obuhvata. Podijelimo S0 na četiri manja trouglasta područja, spajajući sredine stranica originalnog trougla segmentima. Uklonimo unutrašnjost male centralne trokutaste površine. Nazovimo preostali skup S1 (slika 1.2.2). Zatim ponavljamo postupak za svaki od tri preostala mala trokuta da bismo dobili sljedeću aproksimaciju S2. Nastavljajući na ovaj način, dobijamo niz ugniježđenih skupova Sn čiji presjek formira ubrus S.

Rice. 2.2.2. Konstrukcija Sierpinskog salvete

Očigledno je da je ukupna površina izbačenih dijelova tokom izgradnje tačno jednaka površini originalnog trokuta. U prvom koraku odbacili smo ¼ površine. U sljedećem koraku izbacili smo tri trokuta, svaki s površinom jednakom ¼ 2 površine originalnog. Obrazlažući na ovaj način, uvjereni smo da je ukupan udio odbačene površine:

1/4 + 3*(1/42) + 32*(1/43) + … + 3n-1*(1/4n) + … .

Ovaj iznos je jednak. Stoga možemo tvrditi da preostali skup S, odnosno salveta, ima površinu mjere nula. Ovo čini S “savršenim” skupom, u smislu da dijeli svoj komplement na beskonačan broj trouglastih regija, dok ima nultu debljinu.

Opis rada

Leptiri, naravno, ne znaju ništa o zmijama. Ali ptice koje love leptire znaju za njih. Ptice koje ne prepoznaju dobro zmije češće će...

Ako je okto na latinskom za „osam“, zašto onda oktava sadrži sedam nota?

Oktava je interval između dva najbliža zvuka istog imena: do i do, re i re, itd. Sa stanovišta fizike, "srodstvo" ovih...

Zašto se važni ljudi zovu avgust?

Godine 27. pne. e. Rimski car Oktavijan dobio je titulu Augustus, što na latinskom znači "sveti" (usput, u čast iste figure...

Šta pišu u svemiru?

Čuveni vic kaže: „NASA je potrošila nekoliko miliona dolara da razvije specijalnu olovku koja može pisati u svemiru...

Zašto je osnova života ugljenik?

Poznato je oko 10 miliona organskih (tj. na bazi ugljenika) molekula i samo oko 100 hiljada neorganskih molekula. Osim toga...

Zašto su kvarcne lampe plave?

Za razliku od običnog stakla, kvarc propušta ultraljubičasto svjetlo. IN kvarcne lampe Izvor ultraljubičastog zračenja je plinsko pražnjenje u živinim parama. on...

Zašto ponekad pada kiša, a ponekad kiši?

Sa velikom temperaturnom razlikom, snažno uzlazno strujanje nastaje unutar oblaka. Zahvaljujući njima, kapi mogu dugo ostati u vazduhu i...