1. Moguće je dokazati tvrdnju da ako je u prostoru dat pravougaoni koordinatni sistem OXYZ, onda svaka jednačina prvog stepena sa tri nepoznato x,y,z neophodno i dovoljno definiše određenu ravan u odnosu na ovaj sistem R. Ova jednačina se naziva opšta ravan jednadžba i ima sljedeći pogled:
A X+ B at+ C z+ D= 0 (17)
(uporedi sa opštom jednačinom (15) prave linije na ravni, koja iz ovoga sledi na z = 0) i definiše ravan R, okomito na vektor (A,B,C).
Vektor - normalni vektor ravni R.
Jednačina (17) je ekvivalentna sljedećim jednačinama.
2. Jednačina ravni koja prolazi kroz datu tačku M( x 0, y 0, z 0):
A( X- X 0) + B( at-at 0) + C( z-z 0) = 0.
3. Jednačina ravnine u segmentima
,
Gdje 
; 
; 
.
4. Jednačina ravni koja prolazi kroz tri date bodove, koji ne leži na istoj liniji, zapisuje se kao determinanta
,
Gdje ( X 1 , y 1 , z 1), (X 2 , y 2 , z 2), (X 3 , y 3 , z 3) - koordinate datih tačaka.
Ugao između dvije ravni je definiran kao ugao između njihovih normalnih vektora n 1 i n 2. Otuda uslov paralelnih ravni
R 1 i R 2:
i uslov okomitosti dvije ravni:
A 1 A 2 + B 1 IN 2 + C 1 WITH 2 = 0 .
Primjer 29. Kroz tačku TO(1, -3, 2) nacrtati ravan paralelnu vektorima
a =(1, 2, -3) i b =(2,-1,-1) .
Rješenje. Neka M ( X, at, z) – proizvoljna tačka željene ravni. Vector
KM = (X- 1, at+ 3, z- 2) leži u ovoj ravni i vektori A I b paralelno sa njim. Dakle, vektori KM , a i b su komplanarni. Tada je njihov mješoviti proizvod jednak nuli:
.
Stoga -(x –1) - (y + 3) – 5(z – 2) = 0 ili x+ 7y + 5z + 10 = 0. Ovo je željena jednačina ravnine.
Različite vrste jednačine prave u prostoru
Prava linija u prostoru se može specificirati kao:
1) linije preseka dve nepodudarne i neparalelne ravni R 1 i R 2:
;
2) jednačine prave koja prolazi kroz datu tačku M(X 0 , at 0 , z 0) u smjeru određenom vektorom L = (m, n, str):
,
koji se zove kanonska jednadžba linije u svemiru;
3) jednačine prave koja prolazi kroz dvije date tačke M(X 1 , at 1 , z 1)
I M(x 2 , y 2 , z 2):
;
4) parametarske jednačine:
.
Primjer 30. Svesti jednadžbu prave linije na kanonske i parametarske oblike
.
Rješenje. Prava linija se definiše kao linija preseka dve ravni. Normalni vektori ovih ravni n 1 = (3,1,-2) i n 2 = (4,-7,-1) su okomite na željenu pravu, stoga njihov vektorski proizvod [ n 1 , n 2 ] = L paralelno s njim je vektor [ n 1 , n 2 ] (ili bilo koji kolinearni) se može uzeti kao vektor smjera L željenu pravu liniju.
[n 1 , n 2 ] = 
.
Uzmimo to kao L = 3i + j + 5k. Ostaje pronaći neku tačku na datoj pravoj. Za ovo stavljamo, na primjer, z = 0. Dobijamo
.
Nakon što smo riješili ovaj sistem, nalazimo X = 1, at= - 2. Dakle, tačka TO(1, -2, 0) pripada datoj pravoj, a njena kanonska jednadžba ima oblik
1. Vrste jednadžbi prave na ravni
| Ime | Oznaka |
| Opšta jednačina prave linije na ravni | Ax + Bou + C = 0 okomito na vektor = (A, B) |
| Jednačina prave u segmentima | Gdje je a koordinata točke presjeka prave sa Ox osom, a b je koordinata točke presjeka prave sa Oy osom. |
| Normalna jednadžba prave | xcos j + ysin j - p = 0, p je dužina okomice spuštene od početka do prave linije, a j je ugao koji formira ova okomica sa pozitivnim smjerom ose Ox. |
| Jednačina prave linije sa nagibom |
2. Osnovni zadaci na pravoj liniji u prostoru
| Zadatak | Njegova implementacija |
| Jednačina prave koja prolazi kroz dvije tačke M 1 (x 1, y 1, z 1) i M 2 (x 2, y 2, z 2), |
|
| Ugao između pravih linija na ravni |
|
| Uslov okomitosti i paralelnosti pravih | Dvije prave su paralelne ako je k 1 = k 2. Dvije prave su okomite ako |
| Udaljenost od tačke M(x 0, y 0) do prave linije Ah + Wu + C = 0 |
|
3. Vrste ravninskih jednačina u prostoru
| Ime | Oznaka |
| Jednačina opće ravni | Ax + By + Cz + D = 0, gdje su A, B, C koordinate vektora |
| Jednačina ravnine koja prolazi kroz datu tačku M 0 (x 0, y 0, z 0) je okomita ovaj vektor(A, B, C) | A (x – x 0) + B (y – y 0) + C (z – z 0) = 0. |
| Jednačina ravnine u segmentima | Brojevi a, b, c su tačke preseka ravni sa x, y, z osa, respektivno. |
4. Osnovni problemi na ravni u svemiru
| Zadatak | Njegova implementacija |
| Jednačina ravni koja prolazi kroz tri tačke |
|
| Udaljenost od tačke M 0 (x 0, y 0, z 0) do ravni Ah+Bu+Sz +D =0 |
|
| Ugao između ravnina |
|
| Uslovi za paralelnost i okomitost ravni | Avioni okomito Ako: . avioni, paralelno, Ako |
5. Vrste jednačina prave u prostoru
| Ime | Oznaka |
| Parametarske jednadžbe prave | |
| Kanonske jednadžbe prave |
|
| Opšte jednačine prave u prostoru |
|
, gdje je (m, n, p) vektor smjera prave, a M 0 (x 0, y 0, z 0) je tačka kroz koju prava prolazi.
, gdje je vektor smjera6. Osnovni zadaci na pravoj liniji u prostoru
| Zadatak | Njegova implementacija |
| Jednačina prave u prostoru, prolazeći kroz dvije tačke M 1 (x 1, y 1, z 1) i M 2 (x 2, y 2, z 2) |
|
| Ugao između pravih linija u prostoru |
|
| Uslovi za paralelnost i okomitost pravih u prostoru | prave su paralelne ako linije su okomite ako . |
7. Osnovni zadaci na ravni i pravoj u prostoru
8. Krive drugog reda
| Ime | Formula | Geometrijska interpretacija |
| Elipsa |
|
|
| Krug |
|
|
| Hiperbola |
|
|
|
|
||
| Parabola | at 2 = 2px |
|
|
|
9. Površine drugog reda
| Ime | Formula | Geometrijska interpretacija |
| sfera |
|
|
| eliptični cilindar |
|
|
| hiperbolički cilindar |
|
|
| parabolični cilindar |
|
|
| kornet |
|
|
| elipsoid |
|
|
| jednotrakasti hiperboloid |
| |
| hiperboloid od dva lista |
|
|
| eliptični paraboloid |
|
|
| hiperbolično paraboloid |
|
ili
U ovom modulu student mora izučiti teorijski materijal o predloženom obrazovnih elemenata. (cm. Teorijski materijal u višoj matematici: edukativni materijal za studenta. Deo I. Sastavili: Kalukova O.M., Kosheleva N.N., Nikitina M.G., Pavlova E.S., Emelyanova S.G. - Togliatti: TSU, 2005 i dodatni. književnost)
U tabeli 7 prikazan je raspored izučavanja teorijskog materijala za modul „Analitička geometrija“
Tabela 7
| obuku | teorijski materijal |
|
| Auditorne lekcije | ||
| "Koncept jednačine prave na ravni" | ||
| "Ravan i linija u svemiru" | Teorijski materijal na temu "Elementi teorije skupova" |
|
| "Krive drugog reda" | Teorijski materijal na temu "Elementi teorije grafova" |
|
| "Površine drugog reda" | Teorijski materijal na temu " Svojstvene vrijednosti matrice" |
|
Za sva pitanja obratite se akademskom konsultantu postavljanjem pitanja na forumu obrazovnog portala.
Učenik takođe treba da se upozna tipične zadatke i vježbe modula da dovršite svoju verziju IPD-a (pogledajte Vodič za rješavanje problema: nastavno pomagalo za studente Deo I. Sastavili: Nikitina M.G., Pavlova E.S., - Togliatti: TSU, 2008.)
Tabela 8 prikazuje raspored studija praktična pitanja modul "Analitička geometrija"
Tabela 8
| obuku | Praktične lekcije |
|
| Auditorne lekcije | samostalan rad |
|
| Rješavanje zadataka na temu "Prava linija u avionu" | ||
| Rješavanje zadataka na temu "Ravan i prava u prostoru" | Rješavanje zadataka na temu "Elementi teorije skupova" |
|
| Rješavanje zadataka na temu "Krive drugog reda" | Rješavanje zadataka na temu "Elementi teorije grafova" |
|
| Rješavanje zadataka na temu "Površine drugog reda" | Rješavanje zadataka na temu "Svojstvene vrijednosti matrice" |
|
Za sva pitanja obratite se akademskom konsultantu postavljanjem pitanja na forumu obrazovnog portala ili tokom individualnih konsultacija (raspored individualnih konsultacija je predstavljen na obrazovnom portalu).
Učenik mora ispuniti svoju opciju zadaća(vidi Individualni domaći zadatak za studente koji studiraju u tehnologiji 30/70. I deo. Sastavili: Kalukova O.M., Kosheleva N.N., Nikitina M.G., Pavlova E.S., Emelyanova S.G., - Togliatti: TSU, 2005).
Plan implementacije IDZ prikazuje u tabeli 9.
Tabela 9
| Sedmica treninga | |
| od 1 do 4 zadatak |
|
| od 5 do 7 zadataka |
|
| od 8 do 11 zadatak |
|
| 12.13 zadatak |
Na kraju 12. sedmice predajte IDD akademskom konsultantu i primite se na testiranje na obrazovnom portalu
On trinaestu sedmicu Tokom obuke polaznici prolaze modulsko testiranje koje je utvrđeno rasporedom.
Sve jednadžbe ravni, o kojima se govori u narednim paragrafima, mogu se dobiti iz opšte jednačine ravnine, a također se svede na opšta jednačina avion. Dakle, kada govore o jednačini ravni, misle na opštu jednačinu ravni, osim ako nije drugačije navedeno.
Jednačina ravnine u segmentima.
Pogledajte jednadžbu ravnine 
, gdje su a, b i c realni brojevi različiti od nule, poziva se jednačina ravnine u segmentima.
Ovo ime nije slučajno. Apsolutne vrijednosti brojevi a, b i c jednaki su dužinama segmenata koje ravan seče na koordinatnim osa Ox, Oy i Oz, respektivno, računajući od početka. Predznak brojeva a, b i c označava u kom smjeru (pozitivnom ili negativnom) segmenti trebaju biti ucrtani na koordinatne ose.
Na primjer, ugradimo se pravougaoni sistem koordinate Oxyz ravni definisane jednadžbom ravnine u segmentima 
. Da biste to učinili, označite tačku koja je 5 jedinica udaljena od ishodišta u negativnom smjeru ose apscise, 4 jedinice u negativnom smjeru ose ordinate i 4 jedinice u pozitivnom smjeru aplikativne ose. Ostaje samo povezati ove tačke pravim linijama. Ravan rezultirajućeg trokuta je ravan koja odgovara jednadžbi ravnine u segmentima oblika .
Da dobijete više potpune informacije pogledajte članak jednadžba ravnine u segmentima, prikazuje redukciju jednačine ravnine u segmentima na opštu jednačinu ravni, tamo ćete također pronaći detaljna rješenja tipični primjeri i zadaci.
Jednačina normalne ravni.
Zove se opšta ravan jednadžba oblika jednačina normalne ravni, Ako 
jednako jedan, tj. 
, I .
Često možete vidjeti da je normalna jednačina ravni napisana kao . Ovdje su kosinusi smjera normalnog vektora date ravni jedinične dužine, to jest, a p je nenegativan broj jednak udaljenosti od početka do ravni.
Normalna jednadžba ravnine u pravokutnom koordinatnom sistemu Oxyz definira ravan koja je udaljena od početka za udaljenost p u pozitivnom smjeru vektora normale ove ravni 
. Ako je p=0, tada ravan prolazi kroz početak.
Dajemo primjer jednačine normalne ravni.
Neka je ravan određena u pravougaonom koordinatnom sistemu Oxyz opštom jednačinom ravni forme 
. Ova opšta jednačina ravnine je normalna jednačina ravnine. Zaista, vektor normale ove ravni je 
ima dužinu jednako jedan, jer 
.
Jednadžba ravni u normalnom obliku omogućava vam da pronađete udaljenost od tačke do ravni.
Preporučujemo da detaljnije shvatite ovu vrstu jednadžbe ravnine, pogledate detaljna rješenja tipičnih primjera i problema i naučite kako da svedete opštu jednadžbu na normalnog izgleda. To možete učiniti pozivanjem na članak.
Bibliografija.
- Atanasyan L.S., Butuzov V.F., Kadomtsev S.B., Kiseleva L.S., Poznyak E.G. Geometrija. Udžbenik za 10-11 razred srednje škole.
- Bugrov Ya.S., Nikolsky S.M. Viša matematika. Prvi tom: elementi linearne algebre i analitičke geometrije.
- Ilyin V.A., Poznyak E.G. Analitička geometrija.
12.1. Osnovni koncepti
Površina i njena jednačina
Površina u prostoru se može smatrati lokusom tačaka koje zadovoljavaju neki uslov. Na primjer, sfera polumjera R sa centrom u tački O 1 je geometrijsko mjesto svih tačaka u prostoru koje se nalaze na udaljenosti R od tačke O 1.
Pravougaoni koordinatni sistem Oxyz u prostoru omogućava nam da uspostavimo korespondenciju jedan prema jedan između tačaka u prostoru i trojki brojeva x, y i z - njihovih koordinata. Svojstvo zajedničko svim tačkama na površini može se napisati kao jednačina koja povezuje koordinate svih tačaka na površini.
Jednačina date površine u pravougaonom koordinatnom sistemu Oxyz je jednačina F(x, y, z) = 0 sa tri varijable x, y i z, koju zadovoljavaju koordinate svake tačke koja leži na površini i nije zadovoljena koordinate tačaka, ne leži na ovoj površini. Promenljive x, y i z u površinskoj jednačini nazivaju se trenutnim koordinatama tačaka površine.
Jednačina površine omogućava da se proučavanje geometrijskih svojstava površine zamijeni proučavanjem njene jednačine. Dakle, da bismo saznali da li tačka M 1 (x 1 ;y 1 ;z 1) leži na datoj površini, dovoljno je umesto varijabli u jednadžbu površine zameniti koordinate tačke M 1: ako ove koordinate zadovoljavaju jednačinu, tada tačka leži na površinama, ako ne zadovoljavaju, ne leže.
Jednačina sfere
Nađimo jednačinu sfere poluprečnika R sa centrom u tački O 1 (x 0 ;y 0 ;z 0). Prema definiciji sfere, udaljenost bilo koje njene tačke M(x; y; z) od centra O 1 (x 0 ; y 0 ;z 0) jednaka je poluprečniku R, tj. O 1 M= R. Ali, gdje. dakle,
Ovo je tražena jednačina sfere. Zadovoljavaju ga koordinate bilo koje njegove tačke, a ne zadovoljavaju ga koordinate tačaka koje ne leže na datoj sferi.
Ako se centar sfere Ο 1 poklapa sa ishodištem koordinata, tada jednačina sfere ima oblik .
Ako je data jednadžba oblika F(x;y;z) = 0, onda, općenito govoreći, ona definira određenu površinu u prostoru.
Izraz “općenito govoreći” znači da u nekim slučajevima jednačina F(x; y; z) = 0 možda ne definira površinu, već tačku, liniju ili uopće ne definira nikakvu geometrijsku sliku. Kažu "površina degeneriše".
Dakle, jednadžbu ne zadovoljavaju nikakve realne vrijednosti x, y, z. Jednačinu zadovoljavaju samo koordinate tačaka koje leže na osi Ox (iz jednačine slijedi: y = 0, z = 0, a x je bilo koji broj).
Dakle, površina u prostoru se može definirati geometrijski i analitički. To dovodi do formulisanja dva glavna zadatka:
1. Površina je data kao mjesto tačaka. Naći jednačinu ove površine.
2. Zadana je jednačina F(x;y;z) = 0. Istražiti oblik površine definirane ovom jednačinom.
Jednačine prave u prostoru
Prava u prostoru se može smatrati linijom presjeka dvije površine (vidi sliku 66) ili kao mjestom tačaka zajedničkih za dvije površine.
Ako 
I 
- jednadžbe dvije površine koje definiraju pravu L, tada koordinate tačaka ove prave zadovoljavaju sistem od dvije jednačine sa tri nepoznate:
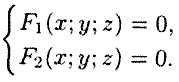(12.1)
Poređenja sistema (12.1) nazivaju se jednačinama prave u prostoru. Na primjer, postoje jednadžbe za Ox osu.
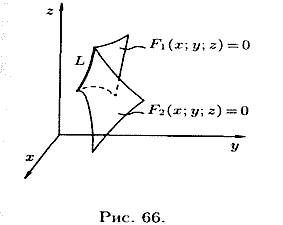
Prava u prostoru se može smatrati putanjom tačke (vidi sliku 67). U ovom slučaju, to je dato vektorskom jednadžbom
ili parametarske jednačine
projekcije vektora (12.2) na koordinatne ose.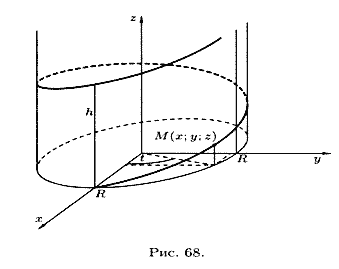 
Na primjer, parametarske jednadžbe zavojnice imaju oblik
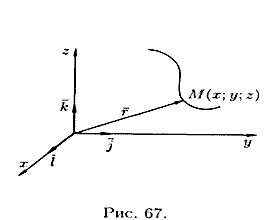
Ako se tačka M kreće jednoliko duž generatrike kružnog cilindra, a sam cilindar rotira jednoliko oko ose, tada tačka M opisuje spiralnu liniju (vidi sliku 68).
12.2. Jednačine ravni u prostoru
Najjednostavnija površina je ravan. Ravan u Oxyz prostoru se može specificirati Različiti putevi. Svaki od njih odgovara određeni tip njene jednačine.
Jednadžba ravni koja prolazi kroz datu tačku okomita na dati vektor
Neka je ravan Q u prostoru Oxyz definirana točkom 
i vektor okomit na ovu ravan (vidi sliku 69). Izvedemo jednačinu ravni Q. Uzmimo proizvoljnu tačku na njoj i sačinimo vektor. Za bilo koju lokaciju tačke M na ravni Q, vektori i su međusobno okomiti, pa su skalarni proizvod jednako nuli: , tj.
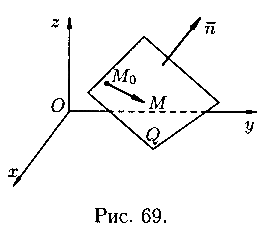(12.3)
Koordinate bilo koje tačke na Q ravni zadovoljavaju jednačinu (12.3), koordinate tačaka koje ne leže na Q ravni ne zadovoljavaju ovu jednačinu (za njih ).
Jednačina (12.3) naziva se jednačina ravnine koja prolazi kroz datu tačku okomito na vektor. Prvog je stepena u odnosu na trenutne koordinate x, y, z. Vektor se naziva normalnim vektorom ravni.
Davanje koeficijenata A, B i C jednačini (12.3) različita značenja, možete dobiti jednadžbu bilo koje ravni koja prolazi kroz tačku . Skup ravnina koje prolaze kroz datu tačku naziva se snop ravnina, a jednačina (12.3) se naziva jednačina snopa ravnina.
Opća jednačina u ravnini
Razmotrimo opštu jednadžbu prvog stepena sa tri varijable x, y i z:
Pod pretpostavkom da barem jedan od koeficijenata A, B ili C nije jednak nuli, na primjer, prepisujemo jednačinu (12.4) u obliku
Upoređujući jednačinu (12.5) sa jednačinom (12.3), vidimo da su jednačine (12.4) i (12.5) jednadžba ravnine sa normalnim vektorom koji prolazi kroz tačku 
.
Dakle, jednačina (12.4) definiše određenu ravan u Oxyz koordinatnom sistemu. Jednačina (12.4) se naziva opšta jednačina ravni.
Posebni slučajevi opće ravnine jednačine:
1. Ako je D = 0, onda ima oblik . Ovu jednačinu zadovoljava točka. Dakle, u ovom slučaju ravan prolazi kroz ishodište.
2. Ako je C = 0, onda imamo jednačinu. Vektor normale je okomit na osu Οz. Prema tome, ravan je paralelna sa Οz osom; ako je B = 0 - paralelno sa Oy osom, A = 0 - paralelno sa Ox osom.
3. Ako je C = D = 0, tada ravan prolazi paralelno sa osom Οz, tj. ravan prolazi kroz osu Οz. Slično, jednačine odgovaraju ravninama koje prolaze kroz ose Ox i Oy, respektivno.
4. Ako je A = B = 0, tada jednačina (12.4) ima oblik , tj. ravan je paralelna sa ravninom Oxy. Slično, jednačine i odgovaraju ravni, respektivno paralelno sa ravnima Oyz i Οxz.
5. Ako je A = B = D = 0, tada će jednačina (12.4) dobiti oblik , tj. z = 0. Ovo je jednačina ravni Oxy. Slično: y = 0 - jednačina ravni Οxz; x = O - jednačina Oyz ravni.
Jednačina ravni koja prolazi kroz tri date tačke
Tri tačke u prostoru koje ne leže na istoj pravoj liniji definišu jednu ravan. Nađimo jednačinu ravni Q koja prolazi kroz tri date tačke M 1 (x 1 ;y 1 ;z 1), M 2 (x 2 ;y 2 ;z 2) i M 3 (x 3 ,y 3 ,z 3), ne leže na istoj pravoj liniji.
Uzmimo proizvoljnu tačku M(x;y;z) na ravni i komponirajmo vektore , , . Ovi vektori leže u Q ravni, stoga su komplanarni. Koristimo uslov koplanarnosti tri vektora (njihov mješoviti proizvod je jednak nuli), dobijamo, tj.
(12.6)
Jednačina (12.6) je jednačina ravni koja prolazi kroz tri date tačke.
Jednačina ravnine u segmentima
Neka ravnina odsiječe segmente na osi Ox, Oy i Oz a, b I c, tj. prolazi kroz tri tačke A(a;0;0), B(0;b;0) I C(0;0;c)(vidi sliku 70). Zamjenom koordinata ovih tačaka u jednačinu (12.6) dobijamo
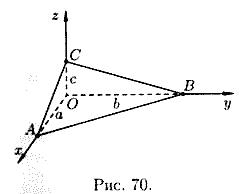
Proširujući determinantu, imamo , tj. ili
(12.7)
Jednačina (12.7) naziva se jednačina ravnine u segmentima na osi. Pogodan je za upotrebu prilikom konstruisanja aviona.
Jednačina normalne ravni
Položaj ravni Q u potpunosti je određen specificiranjem jediničnog vektora koji ima smjer okomite OK, spušten na
ravni od početka i dužine str ova okomita (vidi sliku 71).
Neka je OK = str, i α, β, g su uglovi formirani jediničnim vektorom e sa osama Ox, Oy i Οz. Onda . Uzmimo proizvoljnu tačku M(x; y; z) na ravni i spojimo je sa ishodištem. Formiramo vektor. Za bilo koji položaj tačke M na ravni Q, projekcija vektora radijusa na pravac vektora je uvek jednaka p:, tj.
(12.8)
Jednačina (12.8) se naziva normalna jednačina ravnine u vektorskom obliku. Poznavajući koordinate vektora f i e, prepisujemo jednačinu (12.8) u obliku
Jednačina (12.9) se naziva normalna jednačina ravnine u koordinatnom obliku.
Imajte na umu da se opšta jednačina ravnine (12.4) može svesti na normalnu jednačinu (12.9) na isti način kao što je urađeno za jednačinu prave na ravni. Naime: pomnožite obje strane jednačine (12.4) sa normalizujućim faktorom 
, pri čemu se predznak uzima suprotno od predznaka slobodnog člana D opšte jednačine ravni.
U prethodnom odeljku posvećenom ravni u prostoru, ispitali smo ovo pitanje iz perspektive geometrije. Sada pređimo na opisivanje ravnine pomoću jednačina. Pogled na ravan sa strane algebre uključuje razmatranje glavnih tipova jednačine ravnine u pravougaonom koordinatnom sistemu O x y z trodimenzionalnog prostora.
Yandex.RTB R-A-339285-1
Definicija jednačine ravnine
Definicija 1Avion- Ovo geometrijska figura, koji se sastoji od pojedinačnih tačaka. Svaka tačka u trodimenzionalnom prostoru odgovara koordinatama koje su specificirane sa tri broja. Jednačina ravni uspostavlja odnos između koordinata svih tačaka.
Jednačina ravnine u pravougaonom koordinatnom sistemu 0xz ima oblik jednačine sa tri varijable x, y i z. Koordinate bilo koje tačke koja leži unutar date ravni zadovoljavaju jednačinu; koordinate bilo koje druge tačke koje se nalaze izvan date ravni ne zadovoljavaju.
Zamjena tačke u datoj ravni u jednačinu koordinatne ravni pretvara jednačinu u identitet. Prilikom zamjene koordinata tačke koja leži izvan ravnine, jednačina se pretvara u netačnu jednakost.
Jednačina ravni može imati nekoliko tipova. U zavisnosti od specifičnosti problema koji se rešavaju, jednačina u ravni se može napisati na različite načine.
Jednačina opće ravni
Formulirajmo teoremu, a zatim zapišimo jednadžbu ravnine.
Teorema 1
Bilo koja ravan u pravougaonom koordinatnom sistemu O x y z u trodimenzionalnom prostoru može se odrediti jednačinom oblika A x + B y + C z + D = 0, gde je A, B, C i D– neki realni brojevi koji u isto vrijeme nisu jednaki nuli. Bilo koja jednadžba oblika A x + B y + C z + D = 0 definira ravan u trodimenzionalnom prostoru
Jednačina oblika A x + B y + C z + D = 0 naziva se opšta jednačina ravni. Ako ne priložite brojeve A, B, C I D određene vrijednosti, onda dobijamo jednačinu ravnine u opštem obliku.
Važno je shvatiti da će jednačina λ · A x + λ · B y + λ · C z + λ · D = 0 definirati ravan na potpuno isti način. U jednadžbi, λ je neki realni broj različit od nule. To znači da su jednakosti A x + B y + C z + D = 0 i λ · A x + λ · B y + λ · C z + λ · D = 0 ekvivalentne.
Primjer 1
Opšte jednačine ravnine x - 2 · y + 3 · z - 7 = 0 i - 2 · x + 4 · y - 2 3 · z + 14 = 0 zadovoljavaju koordinate istih tačaka koje se nalaze u tri- dimenzionalni prostor. To znači da oni definiraju istu ravan.
Hajde da damo objašnjenje teoreme o kojoj smo gore govorili. Ravan i njena jednačina su neodvojivi, jer svaka jednačina A x + B y + C z + D = 0 odgovara ravni u datom pravougaonom koordinatnom sistemu, a svakoj ravni koja se nalazi u trodimenzionalnom prostoru odgovara njena jednačina oblika A x + B y + C z + D = 0.
Jednačina ravni A x + B y + C z + D = 0 može biti potpuna ili nepotpuna. Svi koeficijenti A, B, C i D in potpuna jednačina razlikuju se od nule. Inače, opšta jednačina ravnine se smatra nepotpunom.
Planine koje su specificirane nepotpune jednačine, može biti paralelan sa koordinatnim osa, prolaziti kroz koordinatne ose, poklapati se sa koordinatnim ravnima ili se nalaziti paralelno sa njima, prolaziti kroz ishodište koordinata.
Primjer 2
Razmotrimo položaj ravnine u prostoru zadanu jednačinom 4 · y - 5 · z + 1 = 0.
Paralelan je sa x-osi i lociran okomito na ravan O y z. Jednačina z = 0 definiše koordinatnu ravan O y z, a opšta jednačina ravni oblika 3 x - y + 2 z = 0 odgovara ravni koja prolazi kroz početak.
Važno pojašnjenje: koeficijenti A, B i C u opštoj jednačini ravni predstavljaju koordinate vektora normale ravni.
Kada govore o jednačini ravni, misle na opštu jednačinu ravni. Sve vrste jednadžbi ravni, o kojima ćemo govoriti u sljedećem dijelu članka, dobivaju se iz opće jednačine ravnine.
Jednačina normalne ravni
Jednačina normalne ravni je opšta ravanska jednačina oblika A x + B y + C z + D = 0, koja zadovoljava sljedeće uslove: dužina vektora n → = (A, B, C) jednaka je jedan , tj. n → = A 2 + B 2 + C 2 = 1, i D ≤ 0.
Takođe, pisanje normalne jednačine ravni može imati sledeći oblik cos α · x + cos β · y + cos γ · z - p = 0, gde je str je nenegativan broj koji je jednak udaljenosti od početka do ravni, a cos α, cos β, cos γ su kosinusi smjera normalnog vektora date ravni jedinične dužine.
n → = (cos α , cos β , cos γ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1
To jest, prema normalnoj jednadžbi ravni, ravan u pravougaonom koordinatnom sistemu O x y z udaljena je od početka za rastojanje str u pozitivnom pravcu vektora normale ove ravni n → = (cos α, cos β, cos γ). Ako str jednaka nuli, tada ravan prolazi kroz početak.
Primjer 3
Ravan je definisana opštom jednadžbom ravnine oblika - 1 4 · x - 3 4 · y + 6 4 · z - 7 = 0. D = - 7 ≤ 0, vektor normale ove ravni n → = - 1 4, - 3 4, 6 4 ima dužinu jednaku jedan, pošto je n → = - 1 4 2 + - 3 4 2 + 6 4 = 1. Prema tome, ova opšta ravan jednačina je normalna ravan jednačina.
Za detaljnije proučavanje jednačine normalne ravni, preporučujemo da odete u odgovarajući odjeljak. Tema daje analizu problema i tipičnih primjera, kao i metode za dovođenje opšte jednačine ravni u normalni oblik.
Ravan odsijeca segmente određene dužine na koordinatnim osa O x, O y i O z. Dužine segmenata su određene realnim brojevima koji nisu nula a, b i c. Jednačina ravnine u segmentima ima oblik x a + y b + z c = 1. Predznak brojeva a, b i c pokazuje u kom smjeru od nulte vrijednosti treba iscrtati segmente na koordinatnoj osi.
Primjer 4
Konstruirajmo ravan u pravougaonom koordinatnom sistemu, koji je određen jednačinom formule ravni u segmentima x - 5 + y - 4 + z 4 = 1.
Tačke su udaljene od ishodišta u negativnom smjeru za 5 jedinica duž apscisne ose, za 4 jedinice u negativnom smjeru duž ordinatne ose i za 4 jedinice u pozitivnom smjeru duž aplikativne ose. Označite tačke i povežite ih pravim linijama.
Ravan rezultirajućeg trougla je ravan koja odgovara jednadžbi ravni u segmentima, koja ima oblik x - 5 + y - 4 + z 4 = 1.
Detaljnije informacije o jednačini ravnine u segmentima i dovođenju jednačine ravnine u segmentima na opštu jednačinu ravni dostupne su u posebnom članku. Postoji i niz rješenja problema i primjera na tu temu.
Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter